
����Ŀ��һ�����������![]() ���������յ�
���������յ�![]() ��������������ʻ����
��������������ʻ����![]() �ľ���Ϊ2007������;������һЩ��վ�����е�
�ľ���Ϊ2007������;������һЩ��վ�����е�![]() �ľ�����100�ı����ĵط��������˳�վ����Щ��վ�ļ�����Ϊ
�ľ�����100�ı����ĵط��������˳�վ����Щ��վ�ļ�����Ϊ![]() �������е�
�������е�![]() �ľ�����223�ı����ĵط�Ҳ�������˳�վ����Щ��վ�ļ�����Ϊ
�ľ�����223�ı����ĵط�Ҳ�������˳�վ����Щ��վ�ļ�����Ϊ![]() �����ó�����ʻ;�е�ÿ��ͣ����Ҫô�ھ�������ļ���
�����ó�����ʻ;�е�ÿ��ͣ����Ҫô�ھ�������ļ���![]() �еij�վͣ����Ҫô�ھ�������ļ���
�еij�վͣ����Ҫô�ھ�������ļ���![]() �еij�վͣ��������
�еij�վͣ��������![]() ʻ��
ʻ��![]() �����п��ܵ�ͣ����ʽ����Ŀ
�����п��ܵ�ͣ����ʽ����Ŀ![]() �����䣨����������
�����䣨����������
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
���𰸡�C
��������
��![]() ��ʾ��
��ʾ��![]() �ľ�����
�ľ�����![]() �ij�վ����223��3�ַ�ʽ����300��400����4�ַ�ʽ����446��11�ַ�ʽ����500��600����15�ַ�ʽ����669��41�ַ�ʽ����700��800����56�ַ�ʽ����892��153�ַ�ʽ����900��1000��1100����209�ַ�ʽ����1115��780�ַ�ʽ����1200��1300����989�ַ�ʽ����1338��2758�ַ�ʽ����1400��1500����3747�ַ�ʽ����1561��10252�ַ�ʽ����1600��1700����13999�ַ�ʽ����1784��38250�ַ�ʽ����1800��1900��2000����52249�ַ�ʽ����2007��194997�ַ�ʽ��
�ij�վ����223��3�ַ�ʽ����300��400����4�ַ�ʽ����446��11�ַ�ʽ����500��600����15�ַ�ʽ����669��41�ַ�ʽ����700��800����56�ַ�ʽ����892��153�ַ�ʽ����900��1000��1100����209�ַ�ʽ����1115��780�ַ�ʽ����1200��1300����989�ַ�ʽ����1338��2758�ַ�ʽ����1400��1500����3747�ַ�ʽ����1561��10252�ַ�ʽ����1600��1700����13999�ַ�ʽ����1784��38250�ַ�ʽ����1800��1900��2000����52249�ַ�ʽ����2007��194997�ַ�ʽ��


 �������ϵ�д�
�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ��������
��������![]() ��ʼ�մ�������
��ʼ�մ�������![]() ��ʹ��
��ʹ��![]() ����
����![]() �����
���е���![]() ���ϣ�����ʵ��
���ϣ�����ʵ��![]() ��ȡֵ��ΧΪ�� ��
��ȡֵ��ΧΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �Ľ����ֱ�߽���������
�Ľ����ֱ�߽���������![]() ���㣬��ֱ��
���㣬��ֱ��![]() ��б�ʷֱ�Ϊ
��б�ʷֱ�Ϊ![]() ����
����![]() ���м����Ƕ�ֵ���������Ƿ������
���м����Ƕ�ֵ���������Ƿ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� f��x��=ax+��1��a��lnx+![]() ��a��R��
��a��R��
��������a=0ʱ���� f��x���ļ�ֵ��
��������a��0ʱ���� f��x���ĵ������䣻
���������� f��x��=0�ĸ��ĸ����ܷ�ﵽ3�������������ʱa�ķ�Χ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У���֪Բ
�У���֪Բ![]() Բ��Ϊ
Բ��Ϊ![]() ������
������![]() ��б��Ϊ
��б��Ϊ![]() ��ֱ����Բ
��ֱ����Բ![]() �ཻ�ڲ�ͬ������
�ཻ�ڲ�ͬ������![]() ��
��![]() ��
��
��![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��![]() ���Ƿ���ڳ���
���Ƿ���ڳ���![]() ��ʹ������
��ʹ������![]() ��
��![]() ���ߣ�������ڣ���
���ߣ�������ڣ���![]() ֵ����������ڣ���˵�����ɣ�
ֵ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() ����g��x������2����㣬��a��ȡֵ��Χ��
����g��x������2����㣬��a��ȡֵ��Χ��
A. [�C1��0�� B. [0��+�ޣ� C. [�C1��+�ޣ� D. [1��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() Ϊ��Ȼ�����ĵ�����
Ϊ��Ȼ�����ĵ�����
�������ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
������![]() ��֤��������
��֤��������![]() ���������
���������![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() .
.
��1����![]() ��������
��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ���ʣ��Ƿ����ʵ��cʹ��
���ʣ��Ƿ����ʵ��cʹ��![]() ������
������![]() ������֤����Ľ���.
������֤����Ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������P-ABCD�У�ABCDΪ���Σ�AB//CD��BC��AB��AB=2![]() ��BC=
��BC=![]() ��CD=PC=
��CD=PC=![]() ��
��
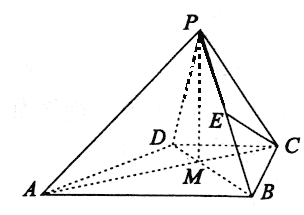
��I����E���߶�PB�ϣ�����CE//ƽ��PAD����![]() ��ֵ��
��ֵ��
��II����֪AC��BD�Ľ���ΪM����PM=1����ƽ��PAC��ƽ��ABCD��������P-BC-Mƽ��ǵ�����ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com