练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f1(x)＝Asin(ωx＋)(A＞0，ω＞0，||＜)的部分图象如下图所示：

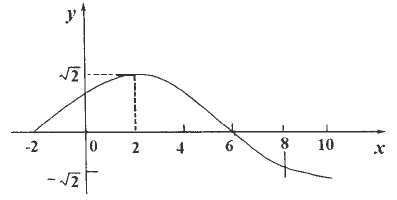
    (1)求此函数的解析式f1(x)；

    (2)与f1(x)的图象关于x＝8对称的函数解析式f2(x)；求f1(x)＋f2(x)单增区间

    答案：
    解析：

    		 　　(1)f1(x)＝ sin( X＋ )

    　　(1)f1(x)＝sin(X＋)

    　　(2)当2kπ－π≤≤2kπ　k∈Z时，即16k－8≤x≤16时，f1(x)＋f2(x)为增函数即单调增区间为[16k－8，16k]k∈Z．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：022

    已知F1，F2是椭圆＋＝1(________)的两个焦点，P是椭圆上一点，且∠F1PF2＝，则△F1PF2的面积是b2．请将题目中空缺的一个可能条件填入“________”处．

    查看答案和解析>>

    科目：高中数学 来源：中学教材标准学案　数学　高二上册 题型：044

    解答题

    已知椭圆的两焦点为F1(－1，0)、F2(1，0)，P为椭圆上一点，且2|F1F2|＝|PF1|＋|PF2|．

    (1)求此椭圆的方程；

    (2)若∠F1PF2＝，求△PF1F2的面积．

    查看答案和解析>>

    科目：高中数学 来源：中学教材标准学案　数学　高二上册 题型：044

    解答题

    已知F1(－3，0)、F2(3，0)分别是椭圆的左、右焦点，P是椭圆上一点，满足PF1⊥PF2，∠F1PF2的平分线交F1F2于M(1，0)，求椭圆的方程．

    查看答案和解析>>

    科目：高中数学 来源：潮阳一中2007届高三摸底考试、文科数学 题型：044

    解答题

    已知焦点在x轴上的双曲线C的两条渐近线过坐标原点，且两条渐近线与以点为圆心，1为半径为圆相切，又知C的一个焦点与A关于直线y＝x对称．

    (1)

    求双曲线C的方程；

    (2)

    若Q是双曲线C上的任一点，F1、F2为双曲线C的左、右两个焦点，从F1引∠F1QF2的平分线的垂线，垂足为N，试求点N的轨迹方程．

    (3)

    设直线y＝mx＋1与双曲线C的左支交于A、B两点，另一直线L经过M(－2，0)及AB的中点，求直线L在y轴上的截距b的取值范围．

    查看答案和解析>>

    同步练习册答案