
【题目】某学校为了解该校教师对教工食堂的满意度情况,随机访问了![]() 名教师.根据这
名教师.根据这![]() 名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为:
名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为: ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() .
.
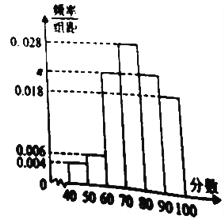
(1)求频率分布直方图中![]() 的值;
的值;
(2)从评分在![]() 的受访教师中,随机抽取2人,求此2人的评分都在
的受访教师中,随机抽取2人,求此2人的评分都在![]() 的概率.
的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据频率分布直方图的性质可知各频率之和为1即可得a=0.022;(2)先计算出受访教师中评分在[50,60)的人数:50×0.006×10=3(人),然后列出所有组合可能即可
解析:(1)因为(0.004+0.006+0.018+a×2+0.028)×10=1,
所以a=0.022
(2)受访教师中评分在[50,60)的有:
50×0.006×10=3(人),记为A1,A2,A3;
受访教师中评分在[40,50)的有:50×0.004×10=2(人),记为B1,B2…8分
从这5名受访教师中随机抽取2人,所有可能的结果共有10种,它们是{A1,A2},{A1,A3},{A1,B1},{A1,B2},{A2,A3},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2}.
又因为所抽取2人的评分都在[50,60)的结果有3种,即{A1,A2},{A1,A3},{A2,A3},故所求的概率为![]() .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】已知P是椭圆![]() 上的一点,F1,F2是椭圆的两个焦点。
上的一点,F1,F2是椭圆的两个焦点。
(1)当∠F1PF2=60°时,求△F1PF2的面积;
(2)当∠F1PF2为钝角时,求点P横坐标的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,正方形![]() 所在的平面与正三角形ABC所在的平面互相垂直,
所在的平面与正三角形ABC所在的平面互相垂直, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
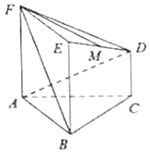
(1)求证: ![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数是数学中重要的概念之一,同学们在初三、高一分别学习过,也知晓其发展过程.1692年,德国数学家莱布尼茨首次使用function这个词,1734年瑞士数学家欧拉首次使用符号f(x)表示函数.1859年我国清代数学家李善兰将function译作函数,“函”意味着信件,巧妙地揭示了对应关系.密码学中的加密和解密其实就是函数与反函数.对自变量恰当地赋值是处理函数问题,尤其是处理抽象函数问题的常用方法之一.请你解答下列问题.
已知函数f(x)满足:对任意的整数a,b均有f(a+b)=f(a) +f(b)+ab+2,且f(-2)=-3.求f(96)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=-3x2+a(6-a)x+6.
(1)解关于a的不等式f(1)>0;
(2)若不等式f(x)>b的解集为(-1,3),求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下命题:
①“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
②命题“若 ![]() ,则
,则 ![]() ”的逆否命题为“若
”的逆否命题为“若 ![]() ,则
,则 ![]() ”;
”;
③对于命题 ![]() :
: ![]() ,使得
,使得 ![]() ,则
,则 ![]() :
: ![]() ,均有
,均有 ![]() ;
;
④若 “![]() 为假命题,则
为假命题,则 ![]() ,
, ![]() 均为假命题;
均为假命题;
其中正确命题的序号为_______________(把所有正确命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是  (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com