
����Ŀ��ij����˾Ϊ����ʵ����Ա���Ľ�����ȫ���᳹���������߹��������Ҫ������ȫ��˾��Χ�ھ���һ���Ҹ��ղ�.Ϊ����Ҫ����960�˵�Ѫ�����л��飬���������϶࣬���߲����ƶ����������ֿɹ�ѡ��ķ���.�����٣���ÿ���˵�Ѫ�ֱ��飬��ʱ��Ҫ��960��.�����ڣ���![]() ����һ�����������飬�Ѵ�ÿ��
����һ�����������飬�Ѵ�ÿ��![]() ���˳�����Ѫ�����һ����м��飬���ÿ���˵�Ѫ��Ϊ���ԣ�������Ľ�������ԣ���
���˳�����Ѫ�����һ����м��飬���ÿ���˵�Ѫ��Ϊ���ԣ�������Ľ�������ԣ���![]() ���˵�Ѫ��ֻ�����һ�Σ���ʱ��Ϊÿ���˵�Ѫ����
���˵�Ѫ��ֻ�����һ�Σ���ʱ��Ϊÿ���˵�Ѫ����![]() �����������������ԣ��������
�����������������ԣ��������![]() ���˵�Ѫ���ٷֱ����һ�λ���.����������
���˵�Ѫ���ٷֱ����һ�λ���.����������![]() ���˵�Ѫ�ܹ���Ҫ����
���˵�Ѫ�ܹ���Ҫ����![]() ��.����˴��ղ���ÿ���˵�Ѫ����������Եĸ���Ϊ
��.����˴��ղ���ÿ���˵�Ѫ����������Եĸ���Ϊ![]() ������Щ��֮������鷴Ӧ�����.
������Щ��֮������鷴Ӧ�����.
��1���跽�����У�ij��![]() ������ÿ���˵�Ѫ�������Ϊ
������ÿ���˵�Ѫ�������Ϊ![]() ����
����![]() �ķֲ��У�
�ķֲ��У�
��2����![]() .�ԱȽϷ������У�
.�ԱȽϷ������У�![]() �ֱ�ȡ2��3��4ʱ�����軯���ƽ���ܴ�������ָ���������ַ�������£���ȷ����٣��������������ƽ�����ٶ��ٴΣ���������������뱣��������.
�ֱ�ȡ2��3��4ʱ�����軯���ƽ���ܴ�������ָ���������ַ�������£���ȷ����٣��������������ƽ�����ٶ��ٴΣ���������������뱣��������.
���𰸡���1���ֲ��м���������2��������.
��������
(1)��![]() ���ܵ�ȡֵΪ
���ܵ�ȡֵΪ![]() ,����ֲ��м���.
,����ֲ��м���.
(2)����(1)�еķֲ���,�ֱ����![]() ʱ����ѧ����,�ٷ��������������Ҫ������ܴ���,�Ӷ��õ������Լ��ٵĴ�������.
ʱ����ѧ����,�ٷ��������������Ҫ������ܴ���,�Ӷ��õ������Լ��ٵĴ�������.
��1����ÿ���˵�Ѫ�����Է�Ӧ�ĸ���Ϊ![]() ,��
,��![]() .
.
����![]() ���˵�Ѫ��Ϻ�����Է�Ӧ�ĸ���Ϊ
���˵�Ѫ��Ϻ�����Է�Ӧ�ĸ���Ϊ![]() ,�����Է�Ӧ�ĸ���Ϊ
,�����Է�Ӧ�ĸ���Ϊ![]() .
.
�������֪![]() ����X�ķֲ���Ϊ��
����X�ķֲ���Ϊ��
|
|
|
|
|
|
��2����������.
��ϣ�1��֪ÿ���˵�ƽ���������Ϊ��
![]() .
.
���Ե�![]() ʱ,
ʱ,![]() ,��ʱ960����Ҫ������ܴ���Ϊ662��,
,��ʱ960����Ҫ������ܴ���Ϊ662��,
![]() ʱ,
ʱ,![]() ,��ʱ960����Ҫ������ܴ���Ϊ580��,
,��ʱ960����Ҫ������ܴ���Ϊ580��,
![]() ʱ,
ʱ,![]() ,��ʱ960����Ҫ����Ĵ�����Ϊ570��,
,��ʱ960����Ҫ����Ĵ�����Ϊ570��,
��![]() ʱ����������,
ʱ����������, ![]() ʱ��������,
ʱ��������, ![]() ʱ�����������.
ʱ�����������.
�����÷��������軯��960��,
���������ַ��������,��ȷ�����,��![]() ʱ�������������ƽ������960-570=390��.
ʱ�������������ƽ������960-570=390��.


 ����5��2���ϵ�д�
����5��2���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��������![]() �ĵ����ԣ���֤��
�ĵ����ԣ���֤��![]() ���ҽ���������㣻
���ҽ���������㣻
������![]() ��
��![]() ��һ����㣬֤������
��һ����㣬֤������![]() �ڵ�
�ڵ�![]() ��������Ҳ������
��������Ҳ������![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������P��ABC������������O��AB�ϣ���PO��ƽ��ABC��2AC![]() AB����������P��ABC�����Ϊ
AB����������P��ABC�����Ϊ![]() �����������Ϊ_____��
�����������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
�У�![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() ��ֱ��
��ֱ��![]() ���۳�
���۳�![]() ������
������![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬���ڷ��۹����У�����˵����������ȷ���ǣ� ��
���е㣬���ڷ��۹����У�����˵����������ȷ���ǣ� ��
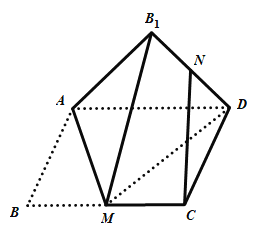
A.����ij��λ�ã�ʹ��![]()
B.���۹����У�![]() �ij��Ƕ�ֵ
�ij��Ƕ�ֵ
C.��![]() ����
����![]()
D.��![]() ��������
��������![]() ��������ʱ������
��������ʱ������![]() �������ı������
�������ı������![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �������ڽ�
�������ڽ�![]() ��
��![]() ��
��![]() ���Եı߷ֱ�Ϊ
���Եı߷ֱ�Ϊ![]() ����
����![]() ��
��![]() .
.
��1����![]() ����
����![]() ��
��![]() �ļн�
�ļн�![]() ��
��
��2����![]() ����
����![]() �ܳ������ֵ.
�ܳ������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijҽԺ���ư�Ѫ���мס������������־�70���������ƺ������������ͳ�ƣ��õ���ȸ�����ͼ��ͼ��ʾ�����в��üס����������Ʒ����Ļ�������֮��Ϊ![]() ��
��
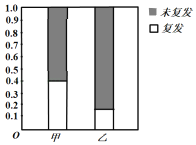
��1����������![]() �������е����ݣ����ж��Ƿ���
�������е����ݣ����ж��Ƿ���![]() ������Ϊ�����������Ʒ����Ի��߰�Ѫ��������Ӱ�죻
������Ϊ�����������Ʒ����Ի��߰�Ѫ��������Ӱ�죻
���� | δ���� | �ܼ� | |
���� | |||
�ҷ��� | 2 | ||
�ܼ� | 70 |
��2��Ϊ�Ľ��������������ֲ�����������5�����߹��ɵ��������������ȡ2������ǡ���Ǹ������ߺ�δ�������߸�1���ĸ��ʣ�
����
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 |
![]() ��
��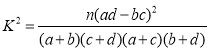 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijʪ�ع������ͼ��һ��ֱ�����Σ����У�![]() ��
��![]() ��
��![]() ��
��![]() ��1ǧ�ף�
��1ǧ�ף�![]() ��
��![]() ǧ�ף�������һ����״�����ε���Ȼ����
ǧ�ף�������һ����״�����ε���Ȼ����![]() ������
������![]() ��
��![]() ��Ϊ�뾶����
��Ϊ�뾶����![]() Ϊ���������ಿ��Ϊ̲�أ�B��D���ǹ��Ľ�����.���������ƻ��ڽ�����֮�佨��һ���۹ⲽ�е����߶�
Ϊ���������ಿ��Ϊ̲�أ�B��D���ǹ��Ľ�����.���������ƻ��ڽ�����֮�佨��һ���۹ⲽ�е����߶�![]() �߶�
�߶�![]() ��
��![]() ������Q���߶�
������Q���߶�![]() �ϣ������߶ζ˵㣩��
�ϣ������߶ζ˵㣩��![]() �뻡
�뻡![]() ������P�㣨���ڻ��˵�ݸ����г�����
������P�㣨���ڻ��˵�ݸ����г�����![]() ��
��![]() �εĽ��������ÿǧ��10��Ԫ�������λ�
�εĽ��������ÿǧ��10��Ԫ�������λ�![]() �Ľ��������ÿǧ��
�Ľ��������ÿǧ��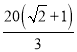 ��Ԫ�����е��Ŀ��Ȳ��ƣ�����
��Ԫ�����е��Ŀ��Ȳ��ƣ�����![]() Ϊ
Ϊ![]() ���ȹ۹ⲽ�е��Ľ������Ϊ
���ȹ۹ⲽ�е��Ľ������Ϊ![]() ��Ԫ.
��Ԫ.
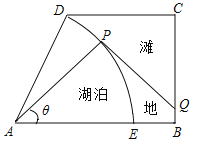
��1�����е��Ľ������![]() ����
����![]() �ĺ�����ϵʽ��������������
�ĺ�����ϵʽ��������������
��2����![]() Ϊ��ֵʱ�����е��Ľ��������ͣ�
Ϊ��ֵʱ�����е��Ľ��������ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC��![]() ��
��![]() �������ҽ���ֱ�Ϊ
�������ҽ���ֱ�Ϊ![]() ��
��![]() ����Բ�ϴ���һ��P������.
����Բ�ϴ���һ��P������.![]() ��
��![]()
��1������ԲC�ı����̣�
��2����֪A��B�ֱ�����ԲC�����Ҷ��㣬��![]() ��ֱ�߽���ԲC��M��N���㣬��ֱ��
��ֱ�߽���ԲC��M��N���㣬��ֱ��![]() ��
��![]() �Ľ���ΪT���Ƿ����һ����ֱ��l��ʹ��T����ֱ��l�ϣ�
�Ľ���ΪT���Ƿ����һ����ֱ��l��ʹ��T����ֱ��l�ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() (
(![]() Ϊ��Ȼ�����ĵ���).
Ϊ��Ȼ�����ĵ���).
(��)����![]() �ĵ������䣻
�ĵ������䣻
(��)��![]() ��
��![]() ��������
��������![]() ��Сֵ�����ֵ.
��Сֵ�����ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com