
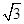 为半径画一弧,分别交AB,AC于D,E.若在△ABC这一平面区域内任丢一粒豆子,则豆子落在扇形ADE内的概率是________.
为半径画一弧,分别交AB,AC于D,E.若在△ABC这一平面区域内任丢一粒豆子,则豆子落在扇形ADE内的概率是________.科目:高中数学 来源:不详 题型:单选题
A.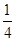 | B. | C.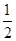 | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
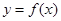 为区间
为区间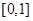 上的连续函数,且恒有
上的连续函数,且恒有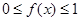 ,可以用随机模拟方法近似计算由曲线
,可以用随机模拟方法近似计算由曲线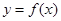 及直线
及直线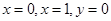 所围成部分的面积
所围成部分的面积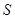 ,先产生两组(每组N个)区间
,先产生两组(每组N个)区间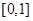 上的均匀随机数
上的均匀随机数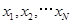 和
和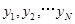 ,由此得到N个点
,由此得到N个点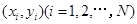 ,再数出其中满足
,再数出其中满足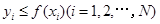 的点数
的点数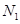 ,那么由随机模拟方案可得
,那么由随机模拟方案可得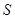 的近似值为 。
的近似值为 。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com