
【题目】判断下列命题是否正确,正确的说明理由,错误的举例说明.
(1)一条直线平行于一个平面,另一条直线与这个平面垂直,则这两条直线互相垂直;
(2)如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 与平面
与平面![]() 所成的二面角和平面
所成的二面角和平面![]() 与平面
与平面![]() 所成的二面角相等或互补;
所成的二面角相等或互补;
(3)如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 平面
平面![]() .
.
科目:高中数学 来源: 题型:
【题目】将圆![]() 上每一点的横坐标保持不变,纵坐标变为原来的
上每一点的横坐标保持不变,纵坐标变为原来的![]() 倍,得曲线
倍,得曲线![]() .
.
![]() 写出
写出![]() 的参数方程;
的参数方程;
![]() 设直线
设直线![]() 与
与![]() 的交点为
的交点为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,求过线段
轴正半轴为极轴建立极坐标系,求过线段![]() 的中点且与
的中点且与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体![]() 中,写出所有
中,写出所有
(1)与直线AB平行的直线,并用“∥”表示;
(2)与直线![]() 异面的直线;
异面的直线;
(3)与直线AB平行的平面,并用合适的符号表示;
(4)与平面![]() 平行的平面,并用合适的符号表示;
平行的平面,并用合适的符号表示;
(5)与直线AD垂直的平面,并用合适的符号表示.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:


(1)证明:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某市举行的一次市质检考试中,为了调查考试试题的有效性以及试卷的区分度,该市教研室随机抽取了参加本次质检考试的500名学生的数学考试成绩,并将其统计如下表所示.

根据上表数据统计,可知考试成绩落在![]() 之间的频率为
之间的频率为![]() .
.
(Ⅰ)求m、n的值;
(Ⅱ)已知本欢质检中的数学测试成绩![]() ,其中
,其中![]() 近似为样本的平均数,
近似为样本的平均数,![]() 近似为样本方差
近似为样本方差![]() ,若该市有4万考生,试估计数学成绩介于
,若该市有4万考生,试估计数学成绩介于![]() 分的人数;
分的人数;![]() 以各组的区间的中点值代表该组的取值
以各组的区间的中点值代表该组的取值![]() Ⅲ
Ⅲ![]() 现按分层抽样的方法从成绩在
现按分层抽样的方法从成绩在![]() 以及
以及![]() 之间的学生中随机抽取12人,再从这12人中随机抽取4人进行试卷分析,记被抽取的4人中成绩在
之间的学生中随机抽取12人,再从这12人中随机抽取4人进行试卷分析,记被抽取的4人中成绩在![]() 之间的人数为X,求X的分布列以及期望
之间的人数为X,求X的分布列以及期望![]() .
.
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
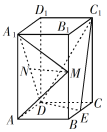
(1)证明:MN∥平面C1DE;
(2)求AM与平面A1MD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点![]() 的直线
的直线![]() 的参数方程是
的参数方程是 (
(![]() 为参数),以平面直角坐标系的原点为极点,
为参数),以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,试问是否存在实数
两点,试问是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果,其中的《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》,有丰富多彩的内容,是了解我国古代数学的重要文献,这5部专著中有3部产生于汉、魏、晋、南北朝时期,某中学拟从这5部专著中选择2部作为“数学文化”校本课程学习内容,则所选2部专著中至少有一部是汉、魏、晋、南北朝时期专著的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]()
(1)若a=1,b=2,求函数在点(2,f(2))处的切线方程;
(2)求函数的单调区间;
(3)若a<b,任取![]() 存在实数m使
存在实数m使![]() 恒成立,求m的取值范围.
恒成立,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com