
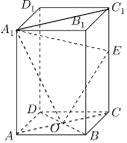
【题目】如图,正四棱柱ABCD﹣A1B1C1D1中,O是BD的中点,E是棱CC1上任意一点.
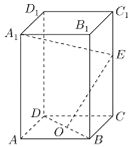
(1)证明:BD⊥A1E;
(2)如果AB=2,![]() ,OE⊥A1E,求AA1的长.
,OE⊥A1E,求AA1的长.
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据正四棱柱性质得AA1⊥平面ABCD,即得AA1⊥BD,根据正方形性质的AC⊥BD,再根据线面垂直判定定理得BD⊥平面ACC1A1,即可得结论;
(2)根据勾股定理列等量关系,解得结果.
(1)证明:连结AC,A1C1,
∵AA1⊥平面ABCD,BD平面ABCD,
∴AA1⊥BD,
∵四边形ABCD是正方形,∴AC⊥BD,
又AC∩AA1=A,AC平面ACC1A1,AA1平面ACC1A1,
∴BD⊥平面ACC1A1,又A1E平面ACC1A1,
∴BD⊥A1E.
(2)∵AB=2,∴AO=CO=![]() ,A1C1=2
,A1C1=2![]() ,
,
设AA1=a,则C1E=a﹣![]() ,
,
∴OE2=4,A1O2=a2+2,A1E2=(a﹣![]() )2+8=a2﹣2
)2+8=a2﹣2![]() a+10,
a+10,
∵OE⊥A1E,
∴A1O2=OE2+A1E2,即a2+2=4+a2﹣2![]() a+10,
a+10,
解得a=![]() .∴AA1=
.∴AA1=![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的两个焦点为
的两个焦点为![]() ,
,![]() ,焦距为
,焦距为![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为弦
为弦![]() 的中点.
的中点.
(1)求椭圆的标准方程;
(2)若直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,
,![]() ,若
,若![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最,编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”,见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注,还得到了无数外国人的关注.某单位有6位外国人,其中关注此次大阅兵的有5位,若从这6位外国人中任意选取2位做一次采访,则被采访者都关注了此次大阅兵的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的四个顶点都在球
的四个顶点都在球![]() 的表面上,
的表面上,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则:(1)球
,则:(1)球![]() 的表面积为__________;(2)若
的表面积为__________;(2)若![]() 是
是![]() 的中点,过点
的中点,过点![]() 作球
作球![]() 的截面,则截面面积的最小值是__________.
的截面,则截面面积的最小值是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在x轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点![]() 为圆心,1为半径的圆相切,又知C的一个焦点与P关于直线
为圆心,1为半径的圆相切,又知C的一个焦点与P关于直线![]() 对称.
对称.
(1)求双曲线C的方程;
(2)设直线![]() 与双曲线C的左支交于A、B两点,另一直线
与双曲线C的左支交于A、B两点,另一直线![]() 经过
经过![]() 及AB的中点,求直线
及AB的中点,求直线![]() 在y轴上的截距b的取值范围;
在y轴上的截距b的取值范围;
(3)若Q是双曲线C上的任一点,![]() 、
、![]() 为双曲线C的左、右两个焦点,从
为双曲线C的左、右两个焦点,从![]() 引
引![]() 的角平分线的垂线,垂足为N,试求点N的轨迹方程.
的角平分线的垂线,垂足为N,试求点N的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com