
【题目】[选修4-5:不等式选讲]已知函数f(x)=log![]() ( |x + 1| + |x- 1|- a ).
( |x + 1| + |x- 1|- a ).
(I)当a=3时,求函数f(x)的定义域;
(Ⅱ)若不等式f(x)![]() 的解集为R,求实数a的最大值.
的解集为R,求实数a的最大值.
【答案】(1){x|x<-![]() 或x>
或x>![]() }.(2)-2
}.(2)-2
【解析】试题分析:(1)先根据绝对值定义将绝对值不等式化为三个不等式组,分别求解,最后求并集,(2)根据绝对值三角不等式可得|x+1|+|x-1|最小值,再解不等式可得实数a的范围,即得a的最大值.
试题解析:解:(I)当a=3时,函数f(x)=log![]() (|x+1|+|x-1|-a)=log
(|x+1|+|x-1|-a)=log![]() (|x+1|+|x-1|-3),
(|x+1|+|x-1|-3),
∴|x+1|+|x-1|-3>0,即|x+1|+|x-1|>3
∴![]() 或
或![]() 或
或![]() .
.
解得x<-![]() 或x>
或x>![]() .
.
故函数的定义域为{x|x<-![]() 或x>
或x>![]() }.
}.
(Ⅱ)若不等式f(x)≥2的解集为R,则f(x)≥2恒成立.
故|x+1|+|x-1|-a≥4恒成立.
∵|x+1|+|x-1|≥|x+1-(x-1)|=2,(当且仅当-1≤x≤1时,取“=”)
∴2-a≥4,故有a≤-2,故实数a的最大值为-2.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C:ρ=2sinθ,A、B为曲线C的两点,以极点为原点,极轴为x轴非负半轴的直角坐标中,曲线E:![]() 是参数)上一点P,则∠APB的最大值为 ( )
是参数)上一点P,则∠APB的最大值为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,动点
,动点![]() 异于原点
异于原点![]() 在y轴上运动,连接FP,过点P作PM交x轴于点M,并延长MP到点N,且
在y轴上运动,连接FP,过点P作PM交x轴于点M,并延长MP到点N,且![]() ,
,![]() .
.
![]() 求动点N的轨迹C的方程;
求动点N的轨迹C的方程;
![]() 若直线l与动点N的轨迹交于A、B两点,若
若直线l与动点N的轨迹交于A、B两点,若![]() 且
且![]() ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ADEF与梯形ABCD所在的平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,M为CE的中点,N为CD中点.
,M为CE的中点,N为CD中点.
![]() 求证:平面
求证:平面![]() 平面ADEF;
平面ADEF;
![]() 求证:平面
求证:平面![]() 平面BDE;
平面BDE;
![]() 求点D到平面BEC的距离.
求点D到平面BEC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某集团为了获得更大的收益,每年要投入一定的资金用于广告促销.经调查投入广告费t(百万元),可增加销售额约为-t2+5t(百万元)(0≤t≤5) (注:收益=销售额-投放).
(1)若该公司将当年的广告费控制在3百万元之内,则应投入多少广告费,才能使该公司由此获得的收益最大?
(2)现该公司准备共投入3百万元,分别用于广告促销和技术改造.经预测,每投入技术改造费x(百万元),可增加的销售额约为-![]() x3+x2+3x(百万元).请设计一个资金分配方案,使该公司由此获得的收益最大.
x3+x2+3x(百万元).请设计一个资金分配方案,使该公司由此获得的收益最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,部分对应值如下表,
,部分对应值如下表,![]() 的导函数
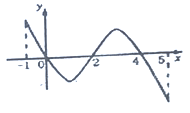
的导函数![]() 的图象如图所示,给出关于
的图象如图所示,给出关于![]() 的下列命题:
的下列命题:
①函数![]() 在
在![]() 处取得极小值;
处取得极小值;
②函数![]() 在
在![]() 是减函数,在
是减函数,在![]() 是增函数;
是增函数;
③当![]() 时,函数
时,函数![]() 有4个零点;
有4个零点;
④如果当![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最小值为0.
的最小值为0.
其中所有的正确命题是__________(写出正确命题的序号).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,△PBC为正三角形,AB⊥平面PBC,AB∥CD,AB=![]() DC,
DC, ![]() .
.
(1)求证:AE∥平面PBC;
(2)求证:AE⊥平面PDC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
(1) 已知![]() ,
,![]() ,
,![]() ,则
,则![]()
(2)将6个相同的小球放入4个不同的盒子中,要求不出现空盒,共有10种放法.
(3) ![]() 被
被![]() 除后的余数为
除后的余数为![]() .
.
(4) 若![]() ,则
,则![]() =
=![]()
(5)抛掷两个骰子,取其中一个的点数为点![]() 的横坐标,另一个的点数为点
的横坐标,另一个的点数为点![]() 的纵坐标,连续抛掷这两个骰子三次,点
的纵坐标,连续抛掷这两个骰子三次,点![]() 在圆
在圆![]() 内的次数
内的次数![]() 的均值为
的均值为![]()
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com