【题目】根据下列条件，求圆的标准方程：
（1）已知点A（1，1），B（﹣1，3），且AB是圆的直径，求圆的标准方程；
（2）圆与y轴交于A（0，﹣4），B（0，﹣2），圆心在直线2x﹣y﹣7＝0上，求圆的方程．
【答案】（1）x2+（y﹣2）2＝2；（2）（x﹣2）2+（y+3）2＝5．
【解析】
（1）求得圆心和半径，进而求得圆的标准方程.
（2）有
两点坐标判断圆心在直线
，解得圆心又在直线
上列方程组，解方程组求得圆心坐标，由两点间距离公式求得圆的半径，进而求得圆的方程.
（1）∵点A（1，1），B（﹣1，3），且AB是圆的直径，
∴圆心坐标为（0，2），半径r
，
∴圆的标准方程为：x2+（y﹣2）2＝2；
（2）∵圆与y轴交于A（0，﹣4），B（0，﹣2），∴圆心在直线y＝﹣3上，
又∵圆心在直线2x﹣y﹣7＝0上，
∴联立方程
，得
，
∴圆心坐标为（2，﹣3），半径r
，
∴圆的标准方程为：（x﹣2）2+（y+3）2＝5．
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案科目：高中数学 来源： 题型：
【题目】已知函数
，在区间
上有最大值
，有最小值
，设
．
（1）求
的值；
（2）不等式
在
时恒成立，求实数
的取值范围；
（3）若方程
有三个不同的实数解，求实数的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿市场销售价与上市时间的关系用图（1）的一条折线表示；西红柿的种植成本与上市时间的关系用图（2）的抛物线段表示.
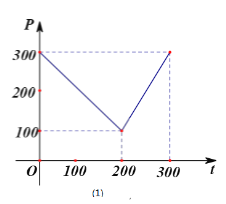
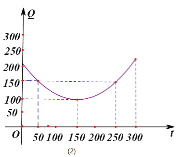
（1）写出图（1）表示的市场售价与时间的函数关系式
；写出图（2）表示的种植成本与时间的函数关系式
；
（2）认定市场售价减去种植成本为纯收益，问何时上市的西红柿收益最大？（注：市场售价和种植成本的单位：元/
kg，时间单位：天.）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE，H是直角项点)来处理污水．管道越长，污水净化效果越好．设计要求管道的接口H是AB的中点，E，F分别落在线段BC，AD上．已知AB＝20米，AD＝
米，记∠BHE＝
．
（1）试将污水净化管道的长度L表示为的函数，并写出定义域；
（2）当取何值时，污水净化效果最好？并求出此时管道的长度L．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在直角坐标系
中，曲线
的参数方程为：
（
为参数），在以
为极点，
轴正半轴为极轴的极坐标系中，曲线
的极坐标方程为
.
（1）求曲线的普通方程和曲线的直角坐标方程；
（2）若曲线与交于
，
两点，点
的坐标为
，求
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点坐标为别为
，
，离心率是
． 椭圆的左、右顶点分别记为
，
．点
是椭圆上位于
轴上方的动点，直线
，
与直线
分别交于
，
两点．
（Ⅰ）求椭圆的方程．
（Ⅱ）求线段
长度的最小值．
（Ⅲ）当线段的长度最小时，在椭圆上的点
满足：
的面积为
．试确定点的个数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
