
����Ŀ��<�л�������������˰��>�涨,����ȫ�¹��ʡ�н�����ò�����3500Ԫ�IJ��ֲ�����˰,����3500Ԫ�IJ���Ϊȫ��Ӧ��˰���ö�,����˰��±��ֶ��ۼƼ���:

(1)��ij��һ�·�Ӧ���ɴ���˰��Ϊ280Ԫ,��ô�����µĹ��ʡ�н�������Ƕ���?
(2)����ij��һ���µĹ��ʡ�н��������![]() Ԫ(0��
Ԫ(0��![]() 10000),�Խ��䵱��Ӧ���ɴ���˰��
10000),�Խ��䵱��Ӧ���ɴ���˰��![]() Ԫ��ʾ�ɹ���
Ԫ��ʾ�ɹ���![]() �ĺ���.
���.
���𰸡�(1)7350Ԫ(2)y=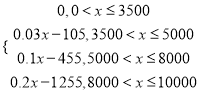
�����������������(1)�����ж�˰��Ϊ280Ԫʱ,��������һ��,�ٽ�����⼴��;
(2)��������ɵ�y=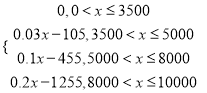 .
.
���������(1)�������µĹ��ʡ�н������Ϊ5000Ԫʱ,
Ӧ��˰(5000-3500)3%=45(Ԫ),�������µĹ��ʡ�н������Ϊ5000��8000Ԫʱ,
Ӧ��˰���Ϊ45+300010%=345(Ԫ),��ij��һ�·�Ӧ���ɴ���˰��Ϊ280Ԫ,
�������µĹ��ʡ�н������Ϊ5000��8000Ԫ,��280-45=235,5000+235��10%=7350(Ԫ),
�������µĹ��ʡ�н��������7350Ԫ.
(2)��0��x![]() 3500ʱ,y=0;
3500ʱ,y=0;
��3500��x![]() 5000ʱ,y=(x-3500)3%=0.03x-105;
5000ʱ,y=(x-3500)3%=0.03x-105;
��5000��x![]() 8000ʱ,y=15003%+(x-5000)10%=0.1x-455;
8000ʱ,y=15003%+(x-5000)10%=0.1x-455;
��8000��x![]() 10000ʱ,y=15003%+300010%+(x-8000)20%=0.2x-1255.
10000ʱ,y=15003%+300010%+(x-8000)20%=0.2x-1255.
���Ͽɵ�,y=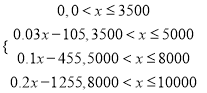
����:�Ժ���Ӧ������Ŀ��飬������κ�������������ʽ��������֪ʶ���㣬�Խ����Ϊ��Ҫ��ʽ���֣���һ�κ��������κ���ģ�͵Ŀ�����Ҫ��������������Ƕȣ�(1)��һ����һ�κ�������κ���ģ�͵Ľ�������ֵ���⣻(2)�Էֶκ�������ʽ����һ�κ����Ͷ��κ�����Ӧ��������Ҫ�������Ķ����⣬��ʵ������ת��Ϊ���������������Ž�


 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x+m|+|2x��1|��m��R����
��1����m=��1ʱ����ʽf��x����2�Ľ⼯��
��2�������x�IJ���ʽf��x����|2x+1|�Ľ⼯ΪA����[1��2]A����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������![]() �У���֪
�У���֪![]() ��
��![]() ��
��

��1����֤��![]() ��
��
��2����![]() ��
��![]() ��һ�㣬��ȷ��
��һ�㣬��ȷ��![]() ��λ�ã�ʹ
��λ�ã�ʹ![]() ƽ��
ƽ��![]() ����˵�����ɣ�
����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ƕ�����
�Ƕ�����![]() �ϵ��溯������
�ϵ��溯������![]() ����
����![]() ��
��![]() ʱ����
ʱ����![]() ����.
����.
�����ж�![]() ��
��![]() �ϵĵ����ԣ���֤����
�ϵĵ����ԣ���֤����
���ⲻ��ʽ![]() ��
��
������![]() �����е�
�����е�![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ����ż������
����ż������
��1����![]() ��ֵ��
��ֵ��
��2��������![]() û����㣬��
û����㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��������![]() ��
�� ![]() ����СֵΪ0����ʵ��
����СֵΪ0����ʵ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����
����![]()
![]() ��
��
��������![]() �ĵ����ݼ����䣻
�ĵ����ݼ����䣻
��������![]() ����
���� ![]() ��ֵ��
��ֵ��
������������![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ����λ�õ�
����λ�õ�![]() ��ͼ��������
��ͼ��������![]() ��
��![]() ������㣬��ʵ��
������㣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x+a|��
��1����a=2�������x�IJ���ʽf��x��+f��x��3����5��
��2��������x�IJ���ʽf��x����f��x+2��+4��|1��3m|���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� ![]() �ϵĵ����ݼ�����
�ϵĵ����ݼ����� ![]() ����
���� ![]() �ĵ���������������
�ĵ��������������� ![]() �������в���ʽ�������ǣ� ��
�������в���ʽ�������ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ����
����![]() ����
����
��1����![]() ʱ���輯��
ʱ���輯��![]() ����
����![]() ��
��
��2���ڣ�1���������£���![]() ��������
��������![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3�����������![]() ������
������![]() ��ʹ����ʽ
��ʹ����ʽ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com