
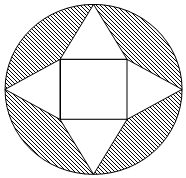
 如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.
如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.| A. | $\frac{4\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{\sqrt{2}}{6}$ |
分析 由折叠前的图形知,底面正方形ABCD,侧面正△PAB,斜高PM,AB:PM=2:$\sqrt{3}$,由 $\frac{1}{2}$AB+PM=(1+$\sqrt{3}$)m,得AB=2m,PM=$\sqrt{3}$m,从而得出四棱锥的高和体积.
解答 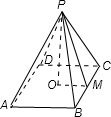 解:如图,在四棱锥P-ABCD中,底面正方形ABCD,侧面正△PBC,
解:如图,在四棱锥P-ABCD中,底面正方形ABCD,侧面正△PBC,
斜高PM,AB:PM=2:$\sqrt{3}$,
且$\frac{1}{2}$AB+PM=(1+$\sqrt{3}$)m,则AB=2m,h=$\sqrt{(\sqrt{3}m)^{2}-{m}^{2}}$=$\sqrt{2}$m,
所以,该四锥体的体积为:V=$\frac{1}{3}$•S正方形ABCD•h=$\frac{1}{3}$•(2m)2•$\sqrt{2}$m=$\frac{4\sqrt{2}}{3}$m3.
故选:A.
点评 本题是通过四棱锥的侧面展开图求其体积,关键是由斜高,高和斜高在底面的射影组成Rt△,求出高,从而求得体积.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{20}+\frac{y^2}{25}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{5}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{20}=1$ | D. | $\frac{x^2}{5}+\frac{y^2}{25}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β | |
| D. | 如果平面α⊥平面β,α∩β=l,过α内任意一点作l的垂线m,则m⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
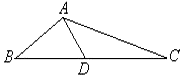 如图所示,在△ABC中,AB=3$\sqrt{6},B=\frac{π}{4}$,D是BC边上一点,且∠ADB=$\frac{π}{3}$
如图所示,在△ABC中,AB=3$\sqrt{6},B=\frac{π}{4}$,D是BC边上一点,且∠ADB=$\frac{π}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [1,2] | C. | [0,1] | D. | (-∞,1]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①③ | C. | ①② | D. | ②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com