[题目]选修4-4:坐标系与参数方程在直线坐标系中.以坐标原点为极点. 轴正半轴为极轴建立极坐标系.直线的参数方程为(为参数).曲线的极坐标方程为.(1)直线的普通方程和曲线的参数方程,(2)设点在上. 在处的切线与直线垂直.求的直角坐标. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】选修4-4：坐标系与参数方程

在直线坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的参数方程为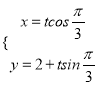（为参数），曲线的极坐标方程为.

（1）直线的普通方程和曲线的参数方程；

（2）设点在上，在处的切线与直线垂直，求的直角坐标.

【答案】（1），（为参数，）（2）或

【解析】试题分析（1）：由，得消去得直线的普通方程，由两边直接乘以得，得出

（2）由（1）知是以为圆心，半径为的圆，设曲线上的点为，因为在处的切线与直线垂直，所以直线与的斜率相等，得，出坐标.

试题解析：

（1）由，得，

消去得直线的普通方程为.

由，

得.将代入上式，

曲线的直角坐标方程为，即.

得曲线的参数方程为（为参数，）

（2）设曲线上的点为，

由（1）知是以为圆心，半径为的圆.

因为在处的切线与直线垂直，所以直线与的斜率相等，

或者，

故得直角坐标为或者.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】下列四组函数中，表示相等函数的一组是（）
A.f（x）=|x|，
B. ，
C. ，g（x）=x+1
D. ，

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）= x2+lnx（其中a≠0）
（1）求f（x）的单调区间；
（2）若f（x）＜﹣ 恒成立，试求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数f（x）=ax﹣（k﹣1）a﹣x（a＞0且a≠1）是定义域为R的奇函数．
（1）求k值；
（2）若f（1）＜0，试判断y=f（x）的单调性并求使不等式f（x2+tx）+f（4﹣x）＜0恒成立的t的取值范围；
（3）若f（1）= ，g（x）=a2x+a﹣2x﹣2f（x），求k∈N+在[1，+∞）上的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数．

（Ⅰ）若函数有零点，其实数的取值范围．

（Ⅱ）证明：当时，．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=lnx﹣ ．
（1）求函数f（x）的单调区间；
（2）设g（x）=﹣x2+2bx﹣4，若对任意x1∈（0，2），x2∈[1，2]，不等式f（x1）≥g（x2）恒成立，求实数b的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】一个人以6米/秒的匀速度去追赶停在交通灯前的汽车，当他离汽车25米时交通灯由红变绿，汽车开始作变速直线行驶（汽车与人的前进方向相同），汽车在时刻t的速度为v（t）=t米/秒，那么，此人（）
A.可在7秒内追上汽车
B.可在9秒内追上汽车
C.不能追上汽车，但其间最近距离为14米
D.不能追上汽车，但其间最近距离为7米

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在△ABC中，a，b，c分别为内角A，B，C的对边，且asinB=﹣bsin（A+ ）．
（1）求A；
（2）若△ABC的面积S= c2 ，求sinC的值．