
 平面
平面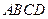 ,
,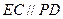 ,且
,且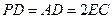 ="2" .
="2" .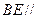 平面
平面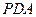 .
.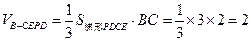
 (2)∵
(2)∵ 平面
平面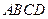 ,
, 平面
平面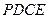
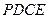
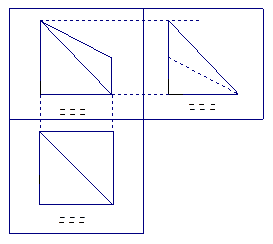
 平面ABCD
平面ABCD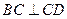 ∴BC
∴BC 平面
平面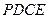 ----------5分
----------5分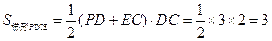 --6分
--6分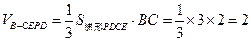 .----8分
.----8分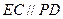 ,
, 平面
平面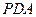 ,
,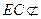 平面
平面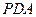
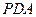 ,------------------------------------10分
,------------------------------------10分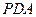 ----------------------------11分
----------------------------11分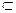 平面EBC,BC
平面EBC,BC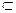 平面EBC且
平面EBC且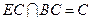
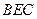 //平面
//平面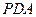 -----------------------------13分
-----------------------------13分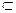 平面EBC ∴BE//平面PDA------------------------------------------14分
平面EBC ∴BE//平面PDA------------------------------------------14分

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
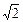 ,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com