
【题目】已知函数![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)讨论函数![]() 的单调性;
的单调性;
(2)用![]() 表示
表示![]() 中较大者,记函数
中较大者,记函数![]() .若函数
.若函数![]() 在
在![]() 上恰有2个零点,求实数a的取值范围.
上恰有2个零点,求实数a的取值范围.
【答案】(1)函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题可得![]() ,结合
,结合![]() 的范围判断
的范围判断![]() 的正负,即可求解;
的正负,即可求解;
(2)结合导数及函数的零点的判定定理,分类讨论进行求解
(1)![]() ,
,
①当![]() 时,
时,![]() ,
,
∴函数![]() 在
在![]() 内单调递增;
内单调递增;
②当![]() 时,令
时,令![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 或
或![]() 时,
时,![]() ,则
,则![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,则
,则![]() 单调递减,
单调递减,
∴函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]()
(2)(Ⅰ)当![]() 时,
时,![]() 所以
所以![]() 在
在![]() 上无零点;
上无零点;
(Ⅱ)当![]() 时,
时,![]() ,
,
①若![]() ,即
,即![]() ,则
,则![]() 是
是![]() 的一个零点;
的一个零点;
②若![]() ,即
,即![]() ,则
,则![]() 不是
不是![]() 的零点
的零点
(Ⅲ)当![]() 时,
时,![]() ,所以此时只需考虑函数
,所以此时只需考虑函数![]() 在
在![]() 上零点的情况,因为
上零点的情况,因为![]() ,所以
,所以
①当![]() 时,
时,![]() 在
在![]() 上单调递增。又
上单调递增。又![]() ,所以
,所以
(ⅰ)当![]() 时,
时,![]() 在
在![]() 上无零点;
上无零点;
(ⅱ)当![]() 时,
时,![]() ,又
,又![]()
![]() ,所以此时
,所以此时![]() 在
在![]() 上恰有一个零点;
上恰有一个零点;
②当![]() 时,令
时,令![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
因为![]() ,
,![]() ,所以此时
,所以此时![]() 在
在![]() 上恰有一个零点,
上恰有一个零点,
综上,![]()


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值?若不存在,说明理由.
的值?若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何学是数学家伯努瓦曼德尔布罗在20世纪70年代创立的一门新的数学学科.它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图1所示的分形规律可得如图2所示的一个树形图:
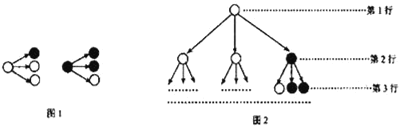
易知第三行有白圈5个,黑圈4个.我们采用“坐标”来表示各行中的白圈、黑圈的个数.比如第一行记为![]() ,第二行记为
,第二行记为![]() ,第三行记为
,第三行记为![]() .照此规律,第
.照此规律,第![]() 行中的白圈、黑圈的“坐标”为
行中的白圈、黑圈的“坐标”为![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
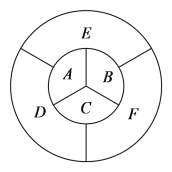
、![]() 六个区域进行染色,每个区域只染一种颜色,每个区域只染一种颜色,且相邻的区域不同色.若有
六个区域进行染色,每个区域只染一种颜色,每个区域只染一种颜色,且相邻的区域不同色.若有![]() 种颜色可供选择,则共有_________种不同的染色方案.
种颜色可供选择,则共有_________种不同的染色方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装加工厂为了提高市场竞争力,对其中一台生产设备提出了甲、乙两个改进方案:甲方案是引进一台新的生产设备,需一次性投资1000万元,年生产能力为30万件;乙方案是将原来的设备进行升级改造,需一次性投入700万元,年生产能力为20万件.根据市场调查与预测,该产品的年销售量的频率分布直方图如图所示,无论是引进新生产设备还是改造原有的生产设备,设备的使用年限均为6年,该产品的销售利润为15元/件(不含一次性设备改进投资费用).
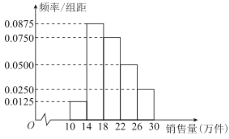
(1)根据年销售量的频率分布直方图,估算年销量的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)将年销售量落入各组的频率视为概率,各组的年销售量用该组区间的中点值作年销量的估计值,并假设每年的销售量相互独立.
①根据频率分布直方图估计年销售利润不低于270万元的概率:
②若以该生产设备6年的净利润的期望值作为决策的依据,试判断该服装厂应选择哪个方案.(6年的净利润=6年销售利润-设备改进投资费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某保险公司的某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 |
|
保费(元) |
|
|
|
|
|
随机调查了该险种的400名续保人在一年内的出险情况,得到下表:
出险次数 | 0 | 1 | 2 | 3 |
|
频数 | 280 | 80 | 24 | 12 | 4 |
该保险公司这种保险的赔付规定如下:
出险序次 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次及以上 |
赔付金额(元) |
|
|
|
| 0 |
将所抽样本的频率视为概率.
(Ⅰ)求本年度续保人保费的平均值的估计值;
(Ⅱ)按保险合同规定,若续保人在本年度内出险3次,则可获得赔付![]() 元;若续保人在本年度内出险6次,则可获得赔付
元;若续保人在本年度内出险6次,则可获得赔付![]() 元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
(Ⅲ)续保人原定约了保险公司的销售人员在上午10:30~11:30之间上门签合同,因为续保人临时有事,外出的时间在上午10:45~11:05之间,请问续保人在离开前见到销售人员的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转,如图,小卢利用图形的旋转设计某次活动的徽标,他将边长为a的正三角形ABC 绕其中心O逆时针旋转到三角形A1B1C1,且![]() .顺次连结A,A1,B,B1,C,C1,A,得到六边形徽标AA1BB1CC1 .
.顺次连结A,A1,B,B1,C,C1,A,得到六边形徽标AA1BB1CC1 .

(1)当=![]() 时,求六边形徽标的面积;
时,求六边形徽标的面积;
(2)求六边形徽标的周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com