
【题目】已知函数f(x)=ln(x+1)+ax2 , a>0.
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在区间(﹣1,0)有唯一零点x0 , 证明: ![]() .
.
【答案】
(1)解:由(1)及f(0)=0可知:仅当极大值等于零,即f(x1)=0时,符合要求.
此时,x1就是函数f(x)在区间(﹣1,0)的唯一零点x0.
所以 ![]() ,从而有
,从而有 ![]() ,
,
又因为 ![]() ,所以
,所以 ![]() ,
,
令x0+1=t,则 ![]() ,
,
设 ![]() ,则
,则 ![]() ,
,
再由(1)知: ![]() ,h'(t)<0,h(t)单调递减,
,h'(t)<0,h(t)单调递减,
又因为 ![]() ,
, ![]() ,
,
所以e﹣2<t<e﹣1,即 ![]()
(2)解:由(1)及f(0)=0可知:仅当极大值等于零,即f(x1)=0时,符合要求.
此时,x1就是函数f(x)在区间(﹣1,0)的唯一零点x0.
所以 ![]() ,从而有
,从而有 ![]() ,
,
又因为 ![]() ,所以
,所以 ![]() ,
,
令x0+1=t,则 ![]() ,
,
设 ![]() ,则
,则 ![]() ,
,
再由(1)知: ![]() ,h'(t)<0,h(t)单调递减,
,h'(t)<0,h(t)单调递减,
又因为 ![]() ,
, ![]() ,
,
所以e﹣2<t<e﹣1,即 ![]()
【解析】(1)求出函数的导数,通过讨论a的范围,求出函数的单调区间;(2)求出 ![]() ,得到
,得到 ![]() ,令x0+1=t,则
,令x0+1=t,则 ![]() ,设
,设 ![]() ,根据函数的单调性证明即可.
,根据函数的单调性证明即可.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】某单位为了了解办公楼用电量y(度)与气温x(℃)之间的关系,随机统计了四个工作日的用电量与当天平均气温,并制作了对照表:
气温(℃) | 17 | 14 | 11 | ﹣2 |
用电量(度) | 23 | 35 | 39 | 63 |
由表中数据得到线性回归方程 ![]() =﹣2x+a,当气温为﹣5℃时,预测用电量约为 ( )
=﹣2x+a,当气温为﹣5℃时,预测用电量约为 ( )
A.38度
B.50度
C.70度
D.30度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接今年6月6日的“全国爱眼日”,某高中学校学生会随机抽取16名学生,经校 医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如右图,若视力测试结果不低于5.0,则称为“好视力”, 
(1)写出这组数据的众数和中位数;
(2)求从这16人中随机选取3人,至少有2人是“好视力”的概率;
(3)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记X表示抽到“好视力”学生的人数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在Rt△AOB中,AO=1,BO=2,如图,动点P是在以O点为圆心,OB为半径的扇形内运动(含边界)且∠BOC=90°;设 ![]() ,则x+y的取值范围 .
,则x+y的取值范围 . 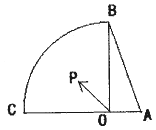
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中, ![]() =
= ![]() +
+ ![]()
(Ⅰ)求△ABM与△ABC的面积之比
(Ⅱ)若N为AB中点, ![]() 与
与 ![]() 交于点P且
交于点P且 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R),求x+y的值.
(x,y∈R),求x+y的值.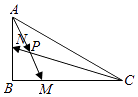
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】底面为正方形的四棱锥S﹣ABCD,且SD⊥平面ABCD,SD= ![]() ,AB=1,线段SB上一M点满足
,AB=1,线段SB上一M点满足 ![]() =
= ![]() ,N为线段CD的中点,P为四棱锥S﹣ABCD表面上一点,且DM⊥PN,则点P形成的轨迹的长度为( )
,N为线段CD的中点,P为四棱锥S﹣ABCD表面上一点,且DM⊥PN,则点P形成的轨迹的长度为( )
A.![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com