
 ,则△ABC为等腰三角形;②已知a, b,c是△ABC的三边长,若
,则△ABC为等腰三角形;②已知a, b,c是△ABC的三边长,若 ,
, ,
, ,则△ABC有两组解;③设
,则△ABC有两组解;③设 ,
,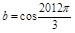 ,
, ,则
,则 ;④将函数
;④将函数 图象向左平移
图象向左平移 个单位,得到函数
个单位,得到函数 图象。其中正确命题的个数是 .
图象。其中正确命题的个数是 . 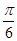 ,
,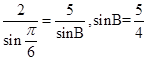 >1,这是不可能的,故②错误;
>1,这是不可能的,故②错误;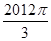 =335×2π+
=335×2π+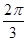 ,∴
,∴ =sin
=sin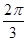 =
=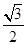 ,同理可得b=cos
,同理可得b=cos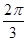 =-
=-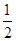 ,c=tan
,c=tan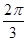 =-
=-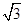 ,故a>b>c,③正确;
,故a>b>c,③正确; 图象向左平移
图象向左平移 个单位,得:y=2sin[3(x+
个单位,得:y=2sin[3(x+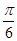 )+
)+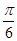 ]
]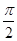 +(3x+
+(3x+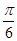 )]=
)]= ,故④正确;
,故④正确;

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com