已知定义在R上的函数f(x)=ax3-2ax2+b(a>0)在区间[-2,1]上的最大值是5,最小值是-11.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若t∈[-1,1]时,f'(x)+tx≤0恒成立,求实数x的取值范围.
分析:(1)对函数f(x)进行求导,令导函数等于0求出x的范围判断函数在[-2,1]上的单调性,进而表示出函数在[-2,1]上的最大值,可求出a的值,确定函数f(x)的解析式.
(2)根据(1)中函数f(x)的导函数将问题f'(x)+tx≤0转化为3x2-4x+tx≤0成立,然后令g(t)=xt+3x2-4x,问题又转化为g(t)≤0在t∈[-1,1]上恒成立,再由一次函数的性质可得到答案.
解答:解:(Ⅰ)∵f(x)=ax
3-2ax
2+b,
∴f'(x)=3ax
2-4ax=ax(3x-4)
令f'(x)=0,得
x1=0,x2=∉[-2,1]因为a>0,所以可得下表:
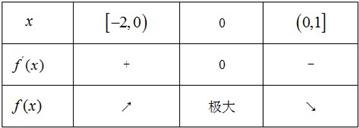
因此f(0)必为最大值,∴f(0)=5,因此b=5,
∵f(-2)=-16a+5,f(1)=-a+5,∴f(1)>f(-2),
即f(-2)=-16a+5=-11,∴a=1,
∴f(x)=x
3-2x
2+5
(Ⅱ)∵f'(x)=3x
2-4x,∴f'(x)+tx≤0等价于3x
2-4x+tx≤0,
令g(t)=xt+3x
2-4x,则问题就是g(t)≤0在t∈[-1,1]上恒成立时,求实数x的取值范围,
为此只需
,即
,
解得0≤x≤1,所以所求实数x的取值范围是[0,1].
点评:本题主要考查函数的求导运算和函数在闭区间上的最值.导数时高考必考题,要重视.




 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案