
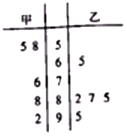
 某校拟举办“成语大赛”,高一(1)班的甲、乙两名同学在本班参加:“成语大赛”选拔测试,在相同的测试条件下,两人5次测试的成绩(单位:分)的茎叶图如图所示:
某校拟举办“成语大赛”,高一(1)班的甲、乙两名同学在本班参加:“成语大赛”选拔测试,在相同的测试条件下,两人5次测试的成绩(单位:分)的茎叶图如图所示:分析 (1)根据茎叶图计算$\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,
比较平均数得出选派乙参赛更好;
(2)根据随机变量X的可能取值,
计算对应的概率,写出分布列,计算数学期望.
解答 解:(1)根据茎叶图知,
$\overline{{x}_{甲}}$=$\frac{1}{5}$×(58+55+76+88+92)=$\frac{369}{5}$,
$\overline{{x}_{乙}}$=$\frac{1}{5}$×(65+82+87+85+95)=$\frac{414}{5}$;
所以乙的平均成绩大于甲的平均成绩,
且乙的成绩成单峰分布,方差较小,
故选派乙参赛更好;
(2)随机变量X的所在可能取值为0,1,2,
P(X=0)=$\frac{{C}_{4}^{1}{•C}_{4}^{1}}{{C}_{5}^{1}{•C}_{5}^{1}}$=$\frac{16}{25}$,
P(X=1)=$\frac{{C}_{2}^{1}{•C}_{4}^{1}}{{C}_{5}^{1}{•C}_{5}^{1}}$=$\frac{8}{25}$,
P(X=2)=$\frac{{C}_{2}^{2}}{{C}_{5}^{1}{•C}_{5}^{1}}$=$\frac{1}{25}$,
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{16}{25}$ | $\frac{8}{25}$ | $\frac{1}{25}$ |
点评 本题考查了茎叶图以及平均数和离散型随机变量的分布列与数学期望问题,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,0) | B. | (0,3) | C. | $(\sqrt{3},0)$ | D. | $(0,\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 2月1日 | 2月2日 | 2月3日 | 2月4日 | 2月5日 |
| 温差x(°C) | 10 | 11 | 13 | 12 | 8 |
| 发芽数x(颗) | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 8 | C. | $\sqrt{17}-1$ | D. | $\sqrt{15}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com