
【题目】随着![]() 业的迅速发展计算机也在迅速更新换代,平板电脑因使用和移动便捷以及时尚新潮性,而备受人们尤其是大学生的青睐,为了解大学生购买平板电脑进行学习的学习情况,某大学内进行了一次匿名调查,共收到1500份有效问卷.调查结果显示700名女学生中有300人,800名男生中有400人拥有平板电脑.
业的迅速发展计算机也在迅速更新换代,平板电脑因使用和移动便捷以及时尚新潮性,而备受人们尤其是大学生的青睐,为了解大学生购买平板电脑进行学习的学习情况,某大学内进行了一次匿名调查,共收到1500份有效问卷.调查结果显示700名女学生中有300人,800名男生中有400人拥有平板电脑.
(Ⅰ)完成下列列联表:
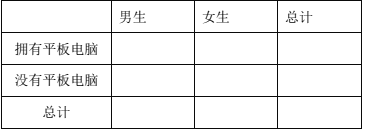
(Ⅱ)分析是否有![]() 的把握认为购买平板电脑与性别有关?
的把握认为购买平板电脑与性别有关?
附:独立性检验临界值表:

(参考公式:![]() ,其中
,其中![]() )
)
科目:高中数学 来源: 题型:
【题目】现从某高中随机抽取部分高二学生,调査其到校所需的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中到校所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() .
.

(1)求直方图中![]() 的值;
的值;
(2)如果学生到校所需时间不少于1小时,则可申请在学校住宿.若该校录取1200名新生,请估计高二新生中有多少人可以申请住宿;
(3)以直方图中的频率作为概率,现从该学校的高二新生中任选4名学生,用![]() 表示所选4名学生中“到校所需时间少于40分钟”的人数,求
表示所选4名学生中“到校所需时间少于40分钟”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数φ(x)= ![]() ,a>0
,a>0
(1)若函数f(x)=lnx+φ(x),在(1,2)上只有一个极值点,求a的取值范围;
(2)若g(x)=|lnx|+φ(x),且对任意x1 , x2∈(0,2],且x1≠x2 , 都有 ![]() <﹣1,求a的取值范围.
<﹣1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() +
+ ![]() =1(a>b>0)的左焦点为F,右顶点为A,离心率为
=1(a>b>0)的左焦点为F,右顶点为A,离心率为 ![]() .已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为
.已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为 ![]() .
.
(Ⅰ)求椭圆的方程和抛物线的方程;
(Ⅱ)设l上两点P,Q关于x轴对称,直线AP与椭圆相交于点B(B异于A),直线BQ与x轴相交于点D.若△APD的面积为 ![]() ,求直线AP的方程.
,求直线AP的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是现代生活进行信息交流的重要工具,据统计,某公司![]() 名员工中
名员工中![]() 的人使用微信,其中每天使用微信时间在一小时以内的有
的人使用微信,其中每天使用微信时间在一小时以内的有![]() ,其余的员工每天使用微信的时间在一小时以上,若将员工分成青年(年龄小于
,其余的员工每天使用微信的时间在一小时以上,若将员工分成青年(年龄小于![]() 岁)和中年(年龄不小于
岁)和中年(年龄不小于![]() 岁)两个阶段,那么使用微信的人中
岁)两个阶段,那么使用微信的人中![]() 是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,那么经常使用微信的员工中
是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,那么经常使用微信的员工中![]() 是青年人.
是青年人.
(1)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出![]() 列联表:
列联表:
青年人 | 中年人 | 总计 | |
经常使用微信 | |||
不经常使用微信 | |||
总计 |
(2)由列联表中所得数据判断,是否有百分之![]() 的把握认为“经常使用微信与年龄有关”?
的把握认为“经常使用微信与年龄有关”?
| 0.010 | 0.001 |
| 6.635 | 10.828 |
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,且圆心在直线
,且圆心在直线![]() :
:![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 的直线与圆
的直线与圆![]() 交于
交于![]() 两点,问在直线
两点,问在直线![]() 上是否存在定点
上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,请求出点
恒成立?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
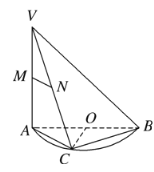
【题目】如图所示,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() 垂直于半圆
垂直于半圆![]() 所在的平面,点
所在的平面,点![]() 是圆周上不同于
是圆周上不同于![]() 的任意一点,
的任意一点,![]() 分别为
分别为![]() 的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( )
A.![]() B.平面
B.平面![]() 平面
平面![]()
C.![]() 与
与![]() 所成的角为45°D.
所成的角为45°D.![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在ABC中,角A,B,C的对边分别为a,b,c,若△ABC为锐角三角形,且满足sinB(1+2cosC)=2sinAcosC+cosAsinC,则下列等式成立的是( )
A.a=2b
B.b=2a
C.A=2B
D.B=2A
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知sin(A+C)=8sin2 ![]() .
.
(Ⅰ)求cosB;
(Ⅱ)若a+c=6,△ABC面积为2,求b.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com