
【题目】已知椭圆![]() 与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为
与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为![]() .
.
(Ⅰ)证明直线AB恒过定点,并求定点的坐标;
(Ⅱ)求三角形ABM的面积的最大值.
【答案】(1)直线![]() 恒过定点
恒过定点![]() .(2)
.(2)![]()
【解析】试题分析:利用设而不求思想设出点的坐标,首先考虑 直线斜率不存在的情况,然后研究直线斜率存在的一般情况,设出直线斜截式方程与椭圆方程联立方程组,代入整理后写出根与系数关系,根据MA、MB的斜率之积为![]() ,代入
,代入![]() ,解出
,解出![]() ,得出直线过定点
,得出直线过定点![]() ,第二步联立方程组后利用判别式大于零,求出k的范围,表示三角形的面积,利用基本不等式求出最值 .
,第二步联立方程组后利用判别式大于零,求出k的范围,表示三角形的面积,利用基本不等式求出最值 .
试题解析:
解:(Ⅰ)由椭圆![]() 的方程得,上顶点
的方程得,上顶点![]() ,记
,记![]() 由题意知,
由题意知, ![]() ,若直线
,若直线![]() 的斜率不存在,则直线
的斜率不存在,则直线![]() 的方程为
的方程为![]() ,故
,故![]() ,且
,且 ,因此
,因此![]() ,与已知不符,因此直线
,与已知不符,因此直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() :
: ![]() ,代入椭圆
,代入椭圆![]() 的方程
的方程![]() 得:
得: ![]()
![]() ………①
………①
因为直线![]() 与曲线
与曲线![]() 有公共点
有公共点![]() ,所以方程①有两个非零不等实根
,所以方程①有两个非零不等实根![]() ,
,
所以![]() ,
,
又![]() ,
, ![]() ,
,
由![]() ,得
,得![]()
即![]()
所以![]()
化简得: ![]() ,故
,故![]() 或
或![]() ,
,
结合![]() 知
知![]() ,
,
即直线![]() 恒过定点
恒过定点![]() .
.
(Ⅱ)由![]() 且
且![]() 得:
得: ![]() 或
或![]() ,
,
又![]()
![]()

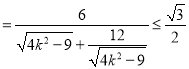 ,当且仅当
,当且仅当![]() ,即
,即![]() 时,
时, ![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】一条光线从点(﹣2,﹣3)射出,经y轴反射后与圆(x+3)2+(y﹣2)2=1相切,则反射光线所在直线的斜率为( )
A.﹣![]() 或﹣
或﹣![]()
B.﹣![]() 或﹣
或﹣![]()
C.﹣![]() 或﹣
或﹣![]()
D.﹣![]() 或﹣
或﹣![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取100名市民,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:
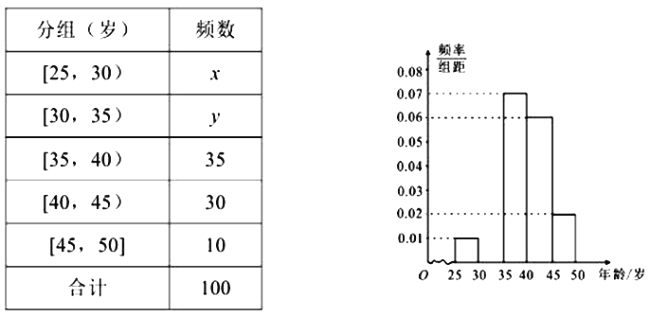
(Ⅰ)求频率分布表中![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(Ⅱ)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加国产手机用户体验问卷调查,现从这20人中随机选取2人各赠送精美礼品一份,设这2名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,且两坐标系有相同的长度单位.已知点
轴的非负半轴为极轴建立极坐标系,且两坐标系有相同的长度单位.已知点![]() 的极坐标为
的极坐标为![]() ,
, ![]() 是曲线
是曲线![]() :
: ![]() 上任意一点,点
上任意一点,点![]() 满足
满足![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若过点![]() 的直线
的直线![]() 的参数方程
的参数方程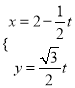 (
(![]() 为参数),且直线
为参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线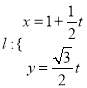 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的极坐标方程为
的极坐标方程为![]() ),圆
),圆![]() 的参数方程为:
的参数方程为: ![]() (其中
(其中![]() 为参数).
为参数).
(1)判断直线![]() 与圆
与圆![]() 的位置关系;
的位置关系;
(2)若椭圆的参数方程为 (
(![]() 为参数),过圆
为参数),过圆![]() 的圆心且与直线
的圆心且与直线![]() 垂直的直线
垂直的直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段: ![]() ,
, ![]() ,
, ![]() ,…
,…![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
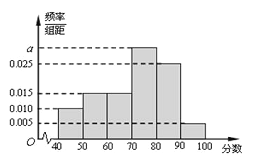
(1)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的中位数(精确到0.1)、众数、平均数;
(2)用分层抽样的方法抽取一个容量为20的样本,求各分数段抽取的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.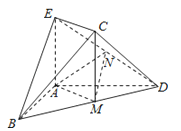
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的是一个几何体的直观图和三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).
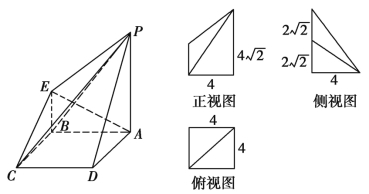
(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com