
����Ŀ����������ָ��![]() �Ǽ�������������Ҫ����������ֵԽ��˵��������Ⱦ״��Խ���أ���������Խ��.ij�ػ�������ͳ���˸õ���ij��1����24������24��Ŀ�������ָ��
�Ǽ�������������Ҫ����������ֵԽ��˵��������Ⱦ״��Խ���أ���������Խ��.ij�ػ�������ͳ���˸õ���ij��1����24������24��Ŀ�������ָ��![]() �����ݵõ������ݻ��Ƴ���ͼ��ʾ������ͼ��������˵��������ǣ� ��
�����ݵõ������ݻ��Ƴ���ͼ��ʾ������ͼ��������˵��������ǣ� ��
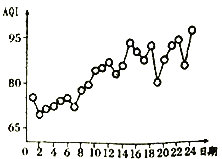
A. �õ����ڸ���2�տ����������
B. �õ����ڸ���24�տ����������
C. �õ����Ӹ���7�յ�12��![]() ��������
��������
D. �õ����Ŀ�������ָ��![]() ��������ڳɸ����
��������ڳɸ����
���𰸡�D
��������
��������ͼ��ÿһ��ѡ����һ�жϵý�.
����ѡ��A, ����2�յĿ�������ָ��![]() ��ͣ����Ըõ����ڸ���2�տ���������ã����Ը�ѡ����ȷ��
��ͣ����Ըõ����ڸ���2�տ���������ã����Ը�ѡ����ȷ��
����ѡ��B, ����24�յĿ�������ָ��![]() ��ߣ����Ըõ����ڸ���24�տ������������Ը�ѡ����ȷ��
��ߣ����Ըõ����ڸ���24�տ������������Ը�ѡ����ȷ��
����ѡ��C,������ͼ�Ͽ����õ����Ӹ���7�յ�12��![]() �����������Ը�ѡ����ȷ��
�����������Ը�ѡ����ȷ��
����ѡ��D,������ͼ�Ͽ����õ����Ŀ�������ָ��![]() ��������ڳ�����أ����Ը�ѡ�����.
��������ڳ�����أ����Ը�ѡ�����.
��ѡ��D


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ⳤΪ2���������У���P��������ĶԽ���AB�ϣ���Q�����������CD�ϣ���PΪ���㣬QΪ���㣬��PQ����СֵΪ_____.
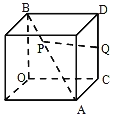
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ����![]() ���ϵ�Բ
���ϵ�Բ![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ��Բ
��Բ![]() .
.
��1����Բ![]() �ı����̣�
�ı����̣�
��2����֪![]() ��Բ
��Բ![]() ��
��![]() ���ཻ������
���ཻ������![]() ����
����![]() �ڵ�
�ڵ�![]() ���Ҳࣩ������
���Ҳࣩ������![]() ����һ����б�Dz�Ϊ0��ֱ����Բ
����һ����б�Dz�Ϊ0��ֱ����Բ![]() �ཻ��
�ཻ��![]() ���㡢�ʣ��Ƿ����ʵ��
���㡢�ʣ��Ƿ����ʵ��![]() ��ʹ��
��ʹ��![]() �������ڣ����ʵ��
�������ڣ����ʵ��![]() ��ֵ���������ڣ���˵�����ɡ�
��ֵ���������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ������ѧϰAPP��ѧϰ���ݰ�������ѧϰ����Ƶѧϰ���࣬��������ѧϰ����Ӱ�죮��֪��APP���ֹ������£�ÿ�Ķ�һƪ���»�1�֣�ÿ������5�֣��ۿ���Ƶ�ۼ�3���ӻ�2�֣�ÿ������6�֣���������ͳ�Ʒ��֣�����ѧϰ���ֵĸ��ʷֲ������1��ʾ����Ƶѧϰ���ֵĸ��ʷֲ������2��ʾ��

��1���������ȡ1���˽�ѧϰ���������ÿ��ѧϰ���ֲ�����9�ֵĸ��ʣ�
��2���������ȡ3���˽�ѧϰ���������ֲ�����9�ֵ�����Ϊ![]() ����
����![]() �ĸ��ʷֲ�����ѧ������
�ĸ��ʷֲ�����ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��������
��������![]() ��
��![]() ��.
��.
����![]() ��
��![]() ��ͼ������ʱ����
��ͼ������ʱ����![]() ��ֵ��
��ֵ��
������![]() ����
����![]() ���ڼ�ֵ����
���ڼ�ֵ����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ⳤΪ1�������������������ֱ��Ϊ�����ᣬ�����ռ�ֱ������ϵ![]() ����
����![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ���߶�
���߶�![]() ��.
��.
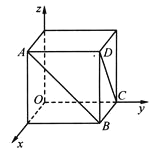
��1����![]() ���ҵ�
���ҵ�![]() ����
����![]() ��ĶԳƵ�Ϊ��
��ĶԳƵ�Ϊ��![]() ʱ����
ʱ����![]() �ij��ȣ�
�ij��ȣ�
��2������![]() ����Խ���
����Խ���![]() ���е㣬��
���е㣬��![]() ����Խ���
����Խ���![]() ���˶�ʱ��̽��
���˶�ʱ��̽��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������P-ABC�У�����P�ڵ���ABC��ͶӰG��ABC�����ģ�PB=BC��2������PBC�����ABC���ɵĶ���ǵĴ�СΪ60��������PABC�������ı����Ϊ______
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ����
����![]() ������
������![]() �ϲ���������
�ϲ���������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ʱ������
ʱ������![]() ��ͼ����
��ͼ����![]() �ύ������
�ύ������![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() �ĵ�����.��������
�ĵ�����.��������![]() ��
��![]() ��������
��������![]() ��
��![]() .�ԱȽ�
.�ԱȽ�![]() ��0�Ĺ�ϵ������������
��0�Ĺ�ϵ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڵ���Ϊ���ε�����S��ABCD�У���֪AD��BC����ASC��60�㣬![]() ��SA��SC��SD��2��
��SA��SC��SD��2��
��1����֤��AC��SD��
��2��������B��SAD�������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com