
【题目】某校共有学生2000人,其中男生1100人,女生900人为了调查该校学生每周平均课外阅读时间,采用分层抽样的方法收集该校100名学生每周平均课外阅读时间(单位:小时)
(1)应抽查男生与女生各多少人?
(2)如图,根据收集100人的样本数据,得到学生每周平均课外阅读时间的频率分布直方图,其中样本数据分组区间为![]() .若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
.若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.

男生 | 女生 | 总计 | |
每周平均课外阅读时间不超过2小时 | |||
每周平均课外阅读时间超过2小时 | |||
总计 |
附: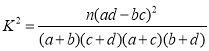
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
【答案】(1)男生人数![]() 人,女生人数:
人,女生人数:![]() 人(2)填表详见解析,有95%的把握认为“该校学生的每周平均阅读时间与性别有关.”
人(2)填表详见解析,有95%的把握认为“该校学生的每周平均阅读时间与性别有关.”
【解析】
(1)由男女生比例以及分层抽样特征,即可求解;(2)由频率分布直方图可得到学生平均每周课外阅读时间超过2小时
(1)男生人数:女生人数=1100:900=11:9
所以,男生人数![]() 人
人
女生人数:![]() 人.
人.
(2)由频率分布直方图可得到学生平均每周课外阅读时间超过2小时的人数为:
![]() 人,
人,
所以,平均每周课外阅读时间超过2小时的男生人数为37人.
可得每周课外阅读时间与性别的列联表为
男生 | 女生 | 总计 | |
每周平均阅读时间不超过2小时 | 18 | 7 | 25 |
每周平均阅读时间超过2小时 | 37 | 38 | 75 |
总计 | 55 | 45 | 100 |
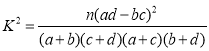
![]()
![]()
![]()
![]()
所以,有95%的把握认为“该校学生的每周平均阅读时间与性别有关.”


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(1)在![]() 中,角A,B,C所对的边分别是a,b,c,证明余弦定理:
中,角A,B,C所对的边分别是a,b,c,证明余弦定理:![]() ;
;
(2)长江某地南北岸平行,如图所示,江面宽度![]() ,一艘游船从南岸码头A出发航行到北岸,假设游船在静水中的航行速度
,一艘游船从南岸码头A出发航行到北岸,假设游船在静水中的航行速度![]() ,水流速度
,水流速度![]() ,设
,设![]() 和
和![]() 的夹角为θ(
的夹角为θ(![]() ),北岸的点
),北岸的点![]() 在点A的正北方向.
在点A的正北方向.
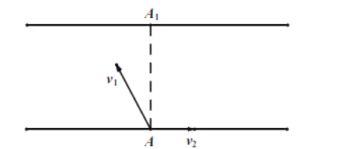
①当![]() 多大时,游船能到达
多大时,游船能到达![]() 处,需要航行多少时间?
处,需要航行多少时间?
②当![]() 时,判断游船航行到达北岸的位置在
时,判断游船航行到达北岸的位置在![]() 的左侧还是右侧,并说明理由.
的左侧还是右侧,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知以C为圆心的圆
中,已知以C为圆心的圆![]() 及其上一点
及其上一点![]() .
.
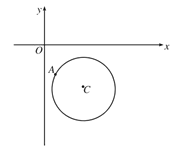
(1)设平行于![]() 的直线
的直线![]() 与圆C相交于
与圆C相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设点![]() 满足:存在圆C上的两点
满足:存在圆C上的两点![]() 使得
使得![]() ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙、丙三个盒子,其中每个盒子中都装有标号分别为1、2、3、4、5、6的六张卡片,现从甲、乙、丙三个盒子中依次各取一张卡片使得卡片上的标号恰好成等差数列的取法数为( )
A.14B.16C.18D.20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的定义域分别为
的定义域分别为![]() ,若存在常数
,若存在常数![]() ,满足:①对任意
,满足:①对任意![]() ,恒有
,恒有![]() ,且
,且![]() .②对任意
.②对任意![]() ,关于
,关于![]() 的不等式组
的不等式组![]()
![]() 恒有解,则称
恒有解,则称![]() 为
为![]() 的一个“
的一个“![]() 型函数”.
型函数”.
(1)设函数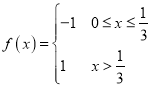 和
和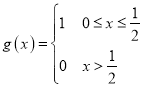 ,求证:
,求证:![]() 为
为![]() 的一个“
的一个“![]() 型函数”;
型函数”;
(2)设常数![]() ,函数
,函数![]() ,
,![]() .若
.若![]() 为
为![]() 的一个“
的一个“![]() 型函数”,求
型函数”,求![]() 的取值范围;
的取值范围;
(3)设函数![]() .问:是否存在常数
.问:是否存在常数![]() ,使得函数
,使得函数![]() 为
为![]() 的一个“
的一个“![]() 型函数”?若存在,求
型函数”?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com