
【题目】(本题满分15分)如图,在四棱锥![]() 中,平面PAD⊥平面ABCD,
中,平面PAD⊥平面ABCD, ![]() ,
,![]() ,E是BD的中点.
,E是BD的中点.

(Ⅰ)求证:EC//平面APD;
(Ⅱ)求BP与平面ABCD所成角的正切值;
(Ⅲ)求二面角![]() 的正弦值.
的正弦值.
【答案】(Ⅰ)详见解析(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
试题分析:(Ⅰ)证明线面平行常用到的思路就是证明平面外的直线平行于平面内的直线(Ⅱ)求BP与平面ABCD所成角首先找到斜线在平面中的射影![]() ,找到所求角
,找到所求角![]() ,通过求解三角形三边得到角的大小(Ⅲ)利用三垂线定理作出二面角的平面角∠PGH,解
,通过求解三角形三边得到角的大小(Ⅲ)利用三垂线定理作出二面角的平面角∠PGH,解![]() 三边即可求得角的正弦值
三边即可求得角的正弦值
试题解析:(Ⅰ)如图,取PA中点F,连结EF、FD,
∵E是BP的中点,∴EF//AB且![]() ,
,
又∵![]() ∴EF
∴EF![]() DC∴四边形EFDC是平行四边形,故得EC//FD 2分
DC∴四边形EFDC是平行四边形,故得EC//FD 2分
又∵EC![]() 平面PAD,FD
平面PAD,FD![]() 平面PAD∴EC//平面ADE 4分
平面PAD∴EC//平面ADE 4分
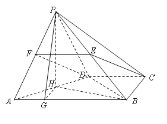
(Ⅱ)取AD中点H,连结PH,因为PA=PD,
所以PH⊥AD
∵平面PAD⊥平面ABCD于AD ∴PH⊥面ABCD
∴HB是PB在平面ABCD内的射影 ∴∠PBH是PB与平面ABCD所成角 6分
∵四边形ABCD中,![]()
∴四边形ABCD是直角梯形,![]()
设AB=2a,则![]() ,在
,在![]() 中,易得
中,易得![]() ,
,![]()
![]() ,又∵
,又∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,![]()
∴![]()
∴在![]() 中,
中,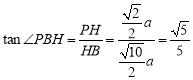 10分
10分
(Ⅲ)在平面ABCD内过点H作AB的垂线交AB于G点,连结PG,则HG是PG在平面ABCD上的射影,故PG⊥AB,所以∠PGH是二面角P-AB-D的平面角,由AB=2a 11分
![]() ,又
,又![]() ∴
∴![]() ,
,
在![]() 中,
中, 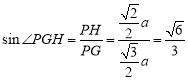
∴二面角P-AB-D的的正弦值为![]() 15分
15分


科目:高中数学 来源: 题型:
【题目】设f(x)=a﹣ ![]() ,x∈R,(其中a为常数).
,x∈R,(其中a为常数).
(1)若f(x)为奇函数,求a的值;
(2)若不等式f(x)+a>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与圆
与圆![]() 相切,且与圆
相切,且与圆![]() 相内切,记圆心
相内切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设![]() 为曲线
为曲线![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交曲线
的平行线交曲线![]() 于
于![]() 、
、![]() 两个不同的点,求
两个不同的点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面结论正确的是( )
①一个数列的前三项是1,2,3,那么这个数列的通项公式![]() .
.
②由平面三角形的性质推测空间四面体的性质,这是一种合理推理.
③在类比时,平面中的三角形与空间中的平行六面体作为类比对象较为合适.
④“所有3的倍数都是9的倍数,某数![]() 一定是9的倍数,则
一定是9的倍数,则![]() 一定是9的倍数”,这是三段论推理,但其结论是错误的.
一定是9的倍数”,这是三段论推理,但其结论是错误的.
A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+2bx+c(b,c∈R).
(1)若函数y=f(x)的零点为﹣1和1,求实数b,c的值;
(2)若f(x)满足f(1)=0,且关于x的方程f(x)+x+b=0的两个实数根分别在区间(﹣3,﹣2),(0,1)内,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C:![]() (m>0)的离心率为
(m>0)的离心率为![]() ,A,B分别为椭圆的左、右顶点,F是其右焦点,P是椭圆C上异于A、B的动点.
,A,B分别为椭圆的左、右顶点,F是其右焦点,P是椭圆C上异于A、B的动点.
(1)求m的值及椭圆的准线方程;
(2)设过点B且与x轴的垂直的直线交AP于点D,当直线AP绕点A转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com