[题目]现采用随机模拟的方法估计某运动员射击4次.至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数.指定0.1表示没有击中目标.2.3.4.5.6.7. 8.9表示击中目标.以4个随机数为一组.代表射击4次的结果.经随机模拟产生了 20组随机数:7527 0293 7140 9857 0347 4373 8636 6947 1417 4698 03 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】现采用随机模拟的方法估计某运动员射击4次，至少击中3次的概率：先由计算器给出0到9之间取整数值的随机数，指定0，1表示没有击中目标，2，3，4，5，6，7， 8，9表示击中目标，以4个随机数为一组，代表射击4次的结果，经随机模拟产生了 20组随机数：

7527 0293 7140 9857 0347 4373 8636 6947 1417 4698

0371 6233 2616 8045 6011 3661 9597 7424 7610 4281

根据以上数据估计该射击运动员射击4次至少击中3次的概率为__________．

【答案】

【解析】

根据数据统计击中目标的次数，再用古典概型概率公式求解.

由数据得射击4次至少击中3次的次数有15，

所以射击4次至少击中3次的概率为.

故答案为：

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，正方体的棱长为，分别是的中点，点在棱

上，（）.

（Ⅰ）三棱锥的体积分别为，当为何值时，最大？最大值为多少？

（Ⅱ）若平面，证明：平面平面.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆的中心在原点，焦点在轴上，为椭圆短轴的一个端点，、为椭圆的左、右焦点，线段的延长线与椭圆相交于点，且.

（1）求椭圆的方程；

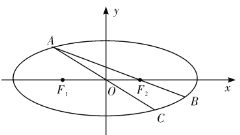
（2）如图，点为椭圆上一动点（非长轴端点），的延长线与椭圆交于点，的延长线与椭圆交于点，求面积的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数.

（Ⅰ）若曲线在点处的切线与直线垂直，求实数的取值；

（Ⅱ）求函数的单调区间；

（Ⅲ）记.当时，函数在区间上有两个零点，求实数的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】用五种不同颜色给三棱台的六个顶点染色，要求每个点染一种颜色，且每条棱的两个端点染不同颜色.则不同的染色方法有___________种.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某果园基地培育出一种特色水果，要在某一季节内采摘一批这种水果销往A市，每售出1吨这种水果获利800元，未售出的水果每吨亏损400元，根据去年市场调研数据统计，该季节A市对这种水果的市场需求量t(单位：吨，100≤t≤150)的频率分布直方图如图所示.现该果园计划采摘140吨这种水果运往A市，经销这种水果的利润Q(单位：元)