
(09年西城区抽样文)(14分)
已知f是直角坐标平面xOy到自身的一个映射,点![]() 在映射f下的象为点
在映射f下的象为点![]() ,记作
,记作![]() .
.
设![]()
![]() ,
,![]() ,
,![]() . 如果存在一个圆,使所有的点
. 如果存在一个圆,使所有的点![]() 都在这个圆内或圆上,那么称这个圆为点
都在这个圆内或圆上,那么称这个圆为点![]() 的一个收敛圆. 特别地,当
的一个收敛圆. 特别地,当![]() 时,则称点
时,则称点![]() 为映射f下的不动点.
为映射f下的不动点.
若点![]() 在映射f下的象为点
在映射f下的象为点![]() .
.
(Ⅰ) 求映射f下不动点的坐标;
(Ⅱ) 若解析:(Ⅰ)解:设不动点的坐标为![]() ,
,
由题意,得 ,解得
,解得![]() ,
,
所以此映射f下不动点为![]() . -----------------------4分
. -----------------------4分
(Ⅱ)证明:由![]() ,得
,得 , --------------------6分
, --------------------6分
所以![]() ,
,
因为![]() ,
,
所以![]() ,
,
所以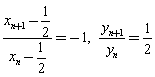 , --------------------------8分
, --------------------------8分
由等比数列定义,得数列![]() N*)是公比为-1,首项为
N*)是公比为-1,首项为![]() 的等比数列,
的等比数列,
所以![]() ,则
,则![]() . --------------------------10分
. --------------------------10分
同理 ![]() .
.
所以 ![]() . -----------------------11分
. -----------------------11分
设![]() ,则
,则![]() ,
, ![]() ------------------12分
------------------12分
因为 ![]() ,
,
所以![]() ,
,
所以![]() .
.
故所有的点![]() 都在以
都在以![]() 为圆心,2为半径的圆内,
为圆心,2为半径的圆内,
即点![]() 存在一个半径为2的收敛圆. ---------------14分
存在一个半径为2的收敛圆. ---------------14分


科目:高中数学 来源: 题型:
(09年西城区抽样文)(14分)
已知函数![]() R).
R).
(Ⅰ) 若a=3,试确定函数![]() 的单调区间;
的单调区间;
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年西城区抽样文)(12分)
甲,乙两人射击,每次射击击中目标的概率分别是![]() . 现两人玩射击游戏,规则如下:若某人某次射击击中目标,则由他继续射击,否则由对方接替射击. 甲、乙两人共射击3次,且第一次由甲开始射击. 假设每人每次射击击中目标与否均互不影响.
. 现两人玩射击游戏,规则如下:若某人某次射击击中目标,则由他继续射击,否则由对方接替射击. 甲、乙两人共射击3次,且第一次由甲开始射击. 假设每人每次射击击中目标与否均互不影响.
(Ⅰ) 求3次射击的人依次是甲、甲、乙,且乙射击未击中目标的概率;
(Ⅱ) 求乙至少有1次射击击中目标的概率.查看答案和解析>>
科目:高中数学 来源: 题型:
(09年西城区抽样文)(14分)
给定抛物线![]() ,F是C的焦点,过点F的直线l与C相交于A、B两点,O为坐标原点.
,F是C的焦点,过点F的直线l与C相交于A、B两点,O为坐标原点.
(Ⅰ)设l的斜率为1,求以AB为直径的圆的方程;
(Ⅱ)设![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年西城区抽样文)(14分)
设函数![]() R)在其图象上一点A
R)在其图象上一点A![]() 处切线的斜率为-1.
处切线的斜率为-1.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)在区间(b-1, b)内的极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com