
某商场经营一批进价是30元/件的商品,在市场试销中发现,此商品销售价 元与日销售量
元与日销售量 件之间有如下关系:
件之间有如下关系:
x | 45 | 50 |
y | 27 | 12 |
(I)确定 与
与 的一个一次函数关系式
的一个一次函数关系式 ;
;
(Ⅱ)若日销售利润为P元,根据(I)中关系写出P关于 的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
(I)y=162-3x(0≤x≤54);(Ⅱ)销售单价为42元/件时,获得最大日销售利润;
【解析】
试题分析:(1)由题意可知 为一次函数,有待定系数法求出解析式;
为一次函数,有待定系数法求出解析式;
(2)销售利润函数=(售价-进价)×销量,代入数值得二次函数,求出最值.
试题解析:(1)因为f(x)为一次函数,设y=ax+b,解方程组
 2分
2分
得a=-3,b=162, 4分
故y=162-3x为所求的函数关系式,
又∵y≥0,∴0≤x≤54. 6分
(2)依题意得:
P=(x-30)·y=(x-30)·(162-3x) 8分
=-3(x-42)2+432. 10分
当x=42时,P最大=432,
即销售单价为42元/件时,获得最大日销售利润. 12分
考点:函数模型的选择与应用.


科目:高中数学 来源:2016届浙江省杭州市外国语学校高一期中考试数学试卷(解析版) 题型:解答题
已知定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,使得
,使得 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的上界.
的上界.
下面我们来考虑两个函数: ,
, .
.
(Ⅰ)当 时,求函数
时,求函数 在
在 上的值域,并判断函数
上的值域,并判断函数 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(Ⅱ)若 ,函数
,函数 在
在 上的上界是
上的上界是 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)若函数 在
在 上是以
上是以 为上界的有界函数, 求实数
为上界的有界函数, 求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016届河南省郑州市高一上学期期末考试数学试卷(解析版) 题型:选择题
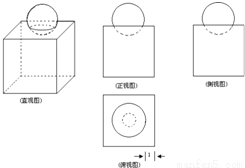
如图是一个简单的组合体的直观图与三视图,一个棱长为4的正方体,正上面中心放一个球,且球的一部分嵌入正方体中,则球的半径是( )
A. 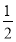 B. 1 C.
B. 1 C. 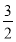 D. 2
D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com