
【题目】若定义在R上的函数![]() 对任意的
对任意的![]() ,都有
,都有![]() 成立,且当
成立,且当![]() 时,
时, ![]() .
.
(1)求![]() 的值;
的值;
(2)求证: ![]() 是R上的增函数;
是R上的增函数;
(3)若![]() ,不等式
,不等式![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|2a≤x<a+3},B={x|x<﹣1或x>5}.
(1)若a=﹣1,求A∪B,(RA)∩B.
(2)若A∩B=,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
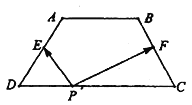
【题目】如图,梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 和
和![]() 分别为
分别为![]() 与
与![]() 的中点,对于常数
的中点,对于常数![]() ,在梯形
,在梯形![]() 的四条边上恰好有8个不同的点
的四条边上恰好有8个不同的点![]() ,使得
,使得![]() 成立,则实数
成立,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,圆
轴的正半轴重合,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为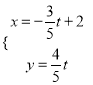 (
(![]() 为参数).
为参数).
(Ⅰ)若![]() ,
, ![]() 是直线
是直线![]() 与
与![]() 轴的交点,
轴的交点, ![]() 是圆
是圆![]() 上一动点,求
上一动点,求![]() 的最大值;
的最大值;
(Ⅱ)若直线![]() 被圆
被圆![]() 截得的弦长等于圆
截得的弦长等于圆![]() 的半径
的半径![]() 倍,求
倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将5个小球放到3个盒子中,在下列条件下,各有多少种投放方法?
①小球不同,盒子不同,盒子不空;
②小球不同,盒子不同,盒子可空;
③小球不同,盒子相同,盒子不空;
④小球不同,盒子相同,盒子可空;
⑤小球相同,盒子不同,盒子不空;
⑥小球相同,盒子不同,盒子可空;
⑦小球相同,盒子相同,盒子不空;
⑧小球相同,盒子相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com