
(06年山东卷文)(12分)
已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,两准线间的距离为l.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线![]() 过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.
过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(06年山东卷文)(12分)
如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=![]() ,PB⊥PD.
,PB⊥PD.
(Ⅰ)求异面直接PD与BC所成角的余弦值;
(Ⅱ)求二面角P-AB-C的大小;
(Ⅲ)设点M在棱PC上,且![]() 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.

查看答案和解析>>
科目:高中数学 来源:2010届高三数学每周精析精练:二项式 题型:选择题
(06年山东卷文)已知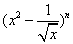 的展开式中第三项与第五项的系数之比为
的展开式中第三项与第五项的系数之比为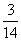 ,则展开式中常数项是( )
,则展开式中常数项是( )
(A)-1 (B)1 (C)-45 (D)45
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com