




 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
3、某化工产品的产量受A、B、C三个因素的影响,每个因素有两个水平,分别用A1,A2,B1,B2,C1,C2表示.分析如图正交试验结果表,得到最佳因素组合(最佳因素组合是指实验结果最大的因素组合)为( )
|
查看答案和解析>>
科目:高中数学 来源: 题型:

| 指针位置 | A区域 | B区域 | C区域 |
| 返存金额(单位:元) | 60 | 30 | 0 |
| 1 |
| 25 |
3
| ||
| 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:
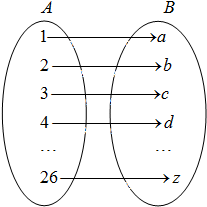 设f是由集合A={x|x∈N,且1≤x≤26}到B={a,b,c,…,z}(即26个英文字母按照字母表顺序排列)的映射,集合B中的任何一个元素在A中也只有唯一的元素与之对应,其对应法则如图所示(依次对齐);又知函数g(x)=
设f是由集合A={x|x∈N,且1≤x≤26}到B={a,b,c,…,z}(即26个英文字母按照字母表顺序排列)的映射,集合B中的任何一个元素在A中也只有唯一的元素与之对应,其对应法则如图所示(依次对齐);又知函数g(x)=
|
查看答案和解析>>
科目:高中数学 来源:2010-2011学年宁夏高三第一次月考理科数学卷 题型:选择题
已知函数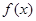 的定义域为[—2,
的定义域为[—2,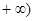 ,部分对应值如下表,
,部分对应值如下表,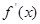 为
为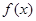 的导函数,函数
的导函数,函数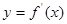 的图象如右图所示:
的图象如右图所示:
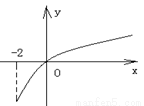
|
|
—2 |
0 |
4 |
|
|
1 |
—1 |
1 |
若两正数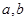 满足
满足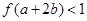 ,则
,则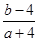 的取值范围是
( )
的取值范围是
( )
A.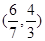 B.
B.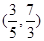 C.
C.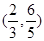 D.
D.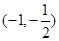
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三上学期数学单元测试7-理科-不等式 题型:选择题
已知函数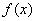 的定义域为[—2,
的定义域为[—2,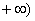 ,部分对应值如下表,
,部分对应值如下表,
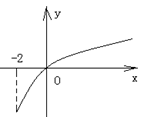
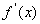 为
为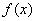 的导函数,函数
的导函数,函数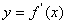 的图象如右图所示:
的图象如右图所示:
|
|
—2 |
0 |
4 |
|
|
1 |
—1 |
1 |
若两正数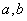 满足
满足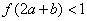 ,则
,则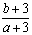 的取值范围是 (
)
的取值范围是 (
)
A.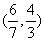 B.
B.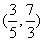 C.
C.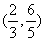 D.
D.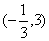
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com