
【题目】已知数列{an}是公差为3的等差数列,数列{bn}是b1=1的等比数列,且![]() .
.
(Ⅰ)分别求数列{an},{bn}的通项公式;
(Ⅱ)令cn= an bn,求数列{cn}的前n项和Tn.
【答案】(1)an=3n-1,bn=![]() ,(2)Tn=
,(2)Tn= ![]() -
- ![]() (6n+7)31-n .
(6n+7)31-n .
【解析】
试题解析:(Ⅰ)∵anbn+1+bn+1=nbn.
当n=1时,a1b2+b2=b1.∵b1=1,b2=![]() , ∴a1=2,
, ∴a1=2,
又∵{an}是公差为3的等差数列, ∴an=3n-1,
∴![]() . 即
. 即![]() .
.
即数列{bn}是以1为首项,以![]() 为公比的等比数列, ∴bn=
为公比的等比数列, ∴bn=![]() ,
,
(Ⅱ)cn= an bn=(3n-1)![]()
∴Tn=2×![]() +5×
+5×![]() +8×
+8×![]() +……+(3n-1)
+……+(3n-1)![]() ①
①
![]() Tn= 2×
Tn= 2×![]() +5×
+5×![]() +8×
+8×![]() +……+(3n-1)
+……+(3n-1)![]() ②
②
① - ②:![]() Tn=2 +3×
Tn=2 +3×![]() +3×
+3×![]() ……+3×
……+3×![]() -(3n-1)
-(3n-1)![]()
=2 + 3×![]() -(3n-1)
-(3n-1)![]()
∴Tn= ![]() -
- ![]() (6n+7)31-n .
(6n+7)31-n .


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式: 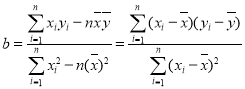 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,
,![]() 是椭圆上一点, 记直线
是椭圆上一点, 记直线![]() 、
、![]() 的斜率为
的斜率为![]() 、
、![]() ,且有
,且有![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点, 以
两点, 以![]() 、
、![]() 为直径的圆经过原点, 且线段
为直径的圆经过原点, 且线段![]() 的垂直平分线在
的垂直平分线在![]() 轴上的截距为
轴上的截距为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
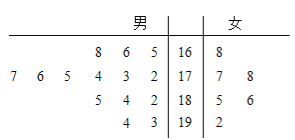
公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
(1)求男生成绩的中位数及女生成绩的平均值;
(2)如果用分层抽样的方法从“甲部门”人选和“乙部门”人选中共选取5人,再从这5人中选2人,那么至少有一人是“甲部门”人选的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在汶川大地震后对唐家山堰塞湖的抢险过程中,武警官兵准备用射击的方法引爆从湖坝上游漂流而下的一个巨大的汽油罐.已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击是相互独立的,且命中的概率都是![]() .
.
(1)求油罐被引爆的概率;
(2)如果引爆或子弹打光则停止射击,设射击次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() .( 结果用分数表示)
.( 结果用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研机构研发了某种高新科技产品,现已进入实验阶段.已知实验的启动资金为10万元,从实验的第一天起连续实验,第![]() 天的实验需投入实验费用为
天的实验需投入实验费用为![]() 元
元![]() ,实验30天共投入实验费用17700元.
,实验30天共投入实验费用17700元.
(1)求![]() 的值及平均每天耗资最少时实验的天数;
的值及平均每天耗资最少时实验的天数;
(2)现有某知名企业对该项实验进行赞助,实验![]() 天共赞助
天共赞助![]() 元
元![]() .为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求
.为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求![]() 的取值范围.(实际耗资=启动资金+试验费用-赞助费)
的取值范围.(实际耗资=启动资金+试验费用-赞助费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com