
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() 的图象与直线
的图象与直线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求实数m的取值范围.
,求实数m的取值范围.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在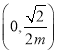 上单调递减,在
上单调递减,在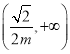 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在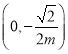 上单调递减,在
上单调递减,在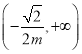 上单调递增;(2)
上单调递增;(2)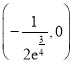 .
.
【解析】
(1)先求导数,根据![]() ,
,![]() 以及
以及![]() 三种情况讨论导函数符号,进而确定对应单调性;
三种情况讨论导函数符号,进而确定对应单调性;
(2)先构造函数![]() ,再求导数,根据
,再求导数,根据![]() 以及
以及![]() 两种情况讨论函数单调性,结合单调性确定满足条件的不等式,解得m的取值范围,最后利用零点存在定理证明所求范围恰好保证函数有两个零点.
两种情况讨论函数单调性,结合单调性确定满足条件的不等式,解得m的取值范围,最后利用零点存在定理证明所求范围恰好保证函数有两个零点.
(1)依题意,![]() ,
,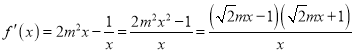 .
.
①若![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上单调递减
上单调递减
②若![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() .
.
(i)若![]() ,则
,则![]() ,
,![]() ,则当
,则当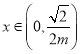 时,
时,![]() ,
,![]() 单调递减,当
单调递减,当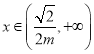 时,
时,![]() ,
,![]() 单调递增;
单调递增;
(ii)若![]() ,则
,则![]() ,
,![]() ,则当
,则当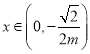 时,
时,![]() ,
,![]() 单调递减,当
单调递减,当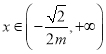 时,
时,![]() ,
,![]() 单调递增.
单调递增.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在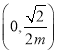 上单调递减,在
上单调递减,在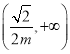 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在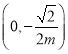 上单调递减,在
上单调递减,在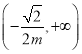 上单调递增.
上单调递增.
(2)令![]() ,则由题意可知
,则由题意可知![]() 有两个大于1的实数根,显然
有两个大于1的实数根,显然![]() .
.
令![]() ,则
,则![]() .
.
若![]() ,则当
,则当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
要满足已知条件,必有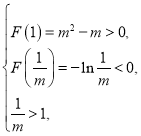 此时无解;
此时无解;
若![]() ,则当
,则当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
要满足已知条件,必有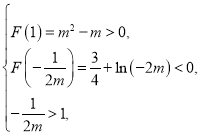 解得
解得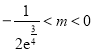 .
.
当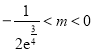 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() ,故函数
,故函数![]() 在
在![]() 上有一个零点.
上有一个零点.
易知![]() ,且
,且![]() ,下证:
,下证:![]() .
.
令![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() ,即
,即![]() ,
,
故![]() ,故
,故![]() ,
,
又![]() 在
在![]() 上单调递增,故
上单调递增,故![]() 在
在![]() 上有一个零点.
上有一个零点.
综上所述,实数m的取值范围为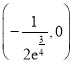 .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AD∥BC,AB=AC=AD=3,PA=BC=4.
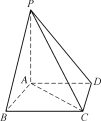
(1)求异面直线PB与CD所成角的余弦值;
(2)求平面PAD与平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 与
与![]() 满足
满足![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和(
项和(![]() ).
).
(1)设数列![]() 是首项和公比都为
是首项和公比都为![]() 的等比数列,且数列
的等比数列,且数列![]() 也是等比数列,求
也是等比数列,求![]() 的值;
的值;
(2)设![]() ,若
,若![]() 且
且![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)设![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ),若存在整数
),若存在整数![]() ,
,![]() ,且
,且![]() ,使得
,使得![]() 成立,求
成立,求![]() 的所有可能值.
的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,直线
,直线![]() 截圆
截圆![]() :
:![]() 与椭圆
与椭圆![]() 所得的弦长之比为
所得的弦长之比为![]() ,椭圆
,椭圆![]() 与
与![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() (
(![]() 且
且![]() )为椭圆
)为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() .试判断
.试判断![]() 是否为定值?若是求出该定值,若不是定值,请说明理由.
是否为定值?若是求出该定值,若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型,在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内.如图所示的小木块中,上面7层为高尔顿板,最下面一层为改造的高尔顿板,小球从通道口落下,第一次与第2层中间的小木块碰撞,以![]() 的概率向左或向右滚下,依次经过6次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前5次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以
的概率向左或向右滚下,依次经过6次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前5次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以![]() 的概率向左滚下,或在前5次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以
的概率向左滚下,或在前5次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以![]() 的概率向右滚下.
的概率向右滚下.

(1)若进行一次高尔顿板试验,求小球落入第7层第6个空隙处的概率;
(2)小明同学在研究了高尔顿板后,利用该图中的高尔顿板来到社团文化节上进行盈利性“抽奖”活动,8元可以玩一次高尔顿板游戏,小球掉入X号球槽得到的奖金为![]() 元,其中
元,其中![]() .
.
(i)求X的分布列:
(ii)高尔顿板游戏火爆进行,很多同学参加了游戏,你觉得小明同学能盈利吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为两非零有理数列(即对任意的
为两非零有理数列(即对任意的![]() ,
,![]() 均为有理数),
均为有理数),![]() 为一无理数列(即对任意的
为一无理数列(即对任意的![]() ,
,![]() 为无理数).
为无理数).
(1)已知![]() ,并且
,并且![]() 对任意的
对任意的![]() 恒成立,试求
恒成立,试求![]() 的通项公式.
的通项公式.
(2)若![]() 为有理数列,试证明:对任意的
为有理数列,试证明:对任意的![]() ,
,![]() 恒成立的充要条件为
恒成立的充要条件为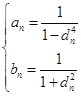 .
.
(3)已知![]() ,
,![]() ,对任意的
,对任意的![]() ,
,![]() 恒成立,试计算
恒成立,试计算![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周脾算经》有记载:一年有二十四个节气,每个节气晷(gui)长损益相同,晷是按照日影测定时刻的仪器,晷长即所测定的影子的长度,二十四节气及晷长变化如图所示,相邻两个节气晷长变化量相同,周而复始,若冬至晷长最长是一丈三尺五寸,夏至晷长最短是一尺五寸,(一丈等于10尺,一尺等于10寸),则秋分节气的晷长是( )
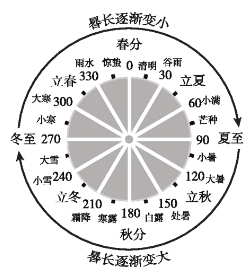
A.七尺五寸B.二尺五寸C.五尺五寸D.四尺五寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com