
【题目】已知椭圆C:![]() ,其中
,其中![]() (e为椭圆离心率),焦距为2,过点M(4,0)的直线l与椭圆C交于点A,B,点B在AM之间.又点A,B的中点横坐标为
(e为椭圆离心率),焦距为2,过点M(4,0)的直线l与椭圆C交于点A,B,点B在AM之间.又点A,B的中点横坐标为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)求直线l的方程.
【答案】(Ⅰ)![]() ,(Ⅱ)y=
,(Ⅱ)y=![]() (x﹣4).
(x﹣4).
【解析】
试题分析:(Ⅰ)运用离心率公式和椭圆的a,b,c的关系,解得a,b,即可得到椭圆方程;
(Ⅱ)设出直线l的方程,联立椭圆方程,消去y,运用判别式大于0,以及韦达定理和中点坐标公式,求出直线的斜率,即可得到所直线方程.
试题解析:(Ⅰ)由条件椭圆C:![]() ,其中
,其中![]() (e为椭圆离心率),焦距为2,可得c=1,a=2,
(e为椭圆离心率),焦距为2,可得c=1,a=2,
故b2=a2﹣c2=3,
椭圆的标准方程是![]() .
.
(Ⅱ)由过点M(4,0)的直线l与椭圆C交于点A,B,点B在AM之间.,可知A,B,M三点共线,
设点A(x1,y1),点B(x2,y2).
若直线AB⊥x轴,则x1=x2=4,不合题意.
当AB所在直线l的斜率k存在时,设直线l的方程为y=k(x﹣4).
由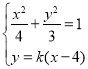 消去y得,(3+4k2)x2﹣32k2x+64k2﹣12=0.①
消去y得,(3+4k2)x2﹣32k2x+64k2﹣12=0.①
由①的判别式△=322k4﹣4(4k2+3)(64k2﹣12)=144(1﹣4k2)>0,
解得k2<![]() ,
,
x1+x2=![]() ,
,
由又点A,B的中点横坐标为![]() .可得
.可得![]()
解得k2=![]() ,即有k=±
,即有k=±![]() .
.
y=![]() (x﹣4).
(x﹣4).
直线l的方程:y=![]() (x﹣4).
(x﹣4).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(导学号:05856287)
已知点A(0,1)与B(![]() ,
, ![]() )都在椭圆C:
)都在椭圆C: ![]() (a>b>0)上,直线AB交x轴于点M.
(a>b>0)上,直线AB交x轴于点M.
(Ⅰ)求椭圆C的方程,并求点M的坐标;
(Ⅱ)设O为原点,点D与点B关于x轴对称,直线AD交x轴于点N.问:y轴上是否存在点E,使得∠OEM=∠ONE?若存在,求点E的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上任意一点到
上任意一点到![]() 的距离比到
的距离比到![]() 轴的距离大1,椭圆
轴的距离大1,椭圆![]() 的中心在原点,一个焦点与
的中心在原点,一个焦点与![]() 的焦点重合,长轴长为4.
的焦点重合,长轴长为4.
(Ⅰ)求曲线![]() 和椭圆
和椭圆![]() 的方程;
的方程;
(Ⅱ)椭圆![]() 上是否存在一点
上是否存在一点![]() ,经过点
,经过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() (
(![]() 为切点)使得直线
为切点)使得直线![]() 过椭圆的上顶点,若存在,求出切线
过椭圆的上顶点,若存在,求出切线![]() 的方程,不存在,说明理由.
的方程,不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856330)
已知等比数列{an}的前n项和为Sn,且a3=4,a3,a4+2,a5成等差数列.数列{![]() }的前n项和为Tn.
}的前n项和为Tn.
(Ⅰ)求数列{an}的通项公式以及前n项和Sn的表达式;
(Ⅱ)若Tn<m对任意n∈N*恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中一年级600名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成![]() 组:[20,30),[30,40),┄,[80,90],并整理得到如下频率分布直方图:
组:[20,30),[30,40),┄,[80,90],并整理得到如下频率分布直方图:
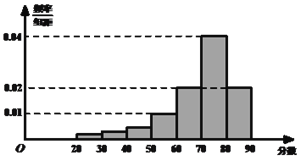
(1)从总体的600名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,
在此几何体中,给出下面四个结论:
①直线BE与直线CF异面; ②直线BE与直线AF异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正确的有( )
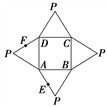
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数f(x)=![]() x3-x满足:对于任意的x1,x2∈[0,2],都有|f(x1)-f(x2)|≤a2恒成立,则a的取值范围是( )
x3-x满足:对于任意的x1,x2∈[0,2],都有|f(x1)-f(x2)|≤a2恒成立,则a的取值范围是( )
A. [-![]() ,
, ![]() ]
]
B. [-![]() ,
, ![]() ]
]
C. (-∞,- ![]() ]∪[
]∪[![]() ,+∞)
,+∞)
D. (-∞,- ![]() ]∪[
]∪[![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
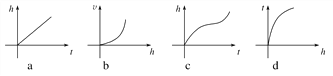
【题目】如图所示,向高为H的水瓶A,B,C,D同时以等速注水,注满为止;
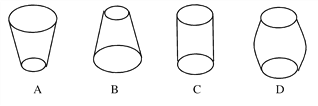
(1)若水深h与注水时间t的函数图象是下图中的a,则水瓶的形状是________;
(2)若水量ν与水深h的函数图像是下图中的b,则水瓶的形状是________;
(3)若水深h与注水时间t的函数图象是下图中的c,则水瓶的形状是________;
(4)若注水时间t与水深h的函数图象是下图中的d,则水瓶的形状是________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知棱长为1的正方体ABCD-A1B1C1D1中,E,F,M分别是线段AB、AD、AA1的中点,又P、Q分别在线段A1B1、A1D1上,且A1P=A1Q=x(0<x<1).设平面MEF∩平面MPQ
=l,现有下列结论:
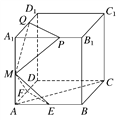
①l∥平面ABCD;
②l⊥AC;
③直线l与平面BCC1B1不垂直;
④当x变化时,l不是定直线.
其中不成立的结论是________.(写出所有不成立结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com