

![]() 内的概率为
内的概率为![]() .
.
(i)当点C在圆周上运动时,求![]() 的最大值;
的最大值;
(ii)记平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
![]() ,当
,当![]() 取最大值时,
取最大值时,
求![]() 的值。
的值。
科目:高中数学 来源: 题型:
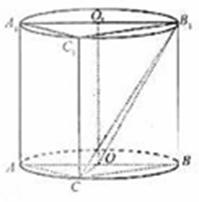
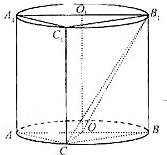 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试、理科数学(福建卷) 题型:044
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.
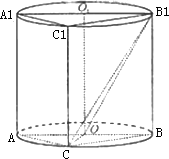
(Ⅰ)证明:平面A1ACC1⊥平面B1BCC1;
(Ⅱ)设AB=AA1,在圆柱OO1内随机选取一点,记该点取自三棱柱ABC-A1B1C1内的概率为p.
(i)当点C在圆周上运动时,求p的最大值;
(ii)圭亚那平面A1ACC1与平面B1OC所成的角为![]() (0°≤90°).当p取最大值时,求cos
(0°≤90°).当p取最大值时,求cos![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年新人教版高三上学期单元测试(3)数学试卷 题型:解答题
(14分)如图,圆柱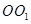 内有一个三棱柱
内有一个三棱柱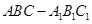 ,三棱柱的 底面为圆柱
,三棱柱的 底面为圆柱
底面的内接三角形,且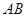 是圆
是圆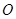 的直径。
的直径。
(I)证明:平面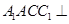 平面
平面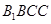 ;
;
(II)设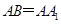 ,在圆柱
,在圆柱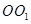 内随机选取一点,记该点取自三棱柱
内随机选取一点,记该点取自三棱柱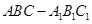 内的概率为
内的概率为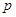 。
。
(i)当点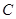 在圆周上运动时,求
在圆周上运动时,求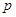 的最大值;
的最大值;
(ii)如果平面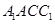 与平面
与平面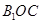 所成的角为
所成的角为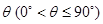 。当
。当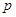 取最大值时,求
取最大值时,求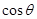 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2011年福建省高二上学期期末考试数学理卷 题型:解答题
.(本小题满分13分)
银河科技有限公司遇到一个技术难题,隧紧急成立甲、乙两个攻关小组,按要求各自独立进行为期一月的技术攻关,同时决定在攻关期满对攻克难题的小组给予奖励,已知这些技术难题在攻关期满时被甲小组攻克的概率为 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 。
。
(I)设 为攻关期满时获奖小组的个数,求
为攻关期满时获奖小组的个数,求 的分布列;
的分布列;
(Ⅱ)设 为攻关期满时获奖小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递减“为事件
在定义域内单调递减“为事件 ,求事件
,求事件 发生的概率。
发生的概率。
查看答案和解析>>
科目:高中数学 来源:2010年高考试题(福建卷)解析版(理) 题型:解答题
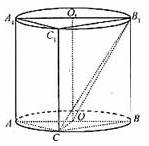 如图,圆柱
如图,圆柱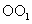 内有一个三棱柱
内有一个三棱柱 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。
(Ⅰ)证明:平面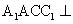 平面
平面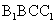 ;
;
(Ⅱ)设AB=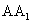 ,在圆柱
,在圆柱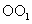 内随机选取一点,记该点取自于三棱柱
内随机选取一点,记该点取自于三棱柱 内的概率为
内的概率为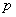 。
。
(i)当点C在圆周上运动时,求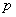 的最大值;
的最大值;
(ii)记平面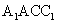 与平面
与平面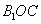 所成的角为
所成的角为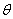
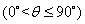 ,当
,当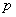 取最大值时,求
取最大值时,求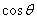 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com