练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面内，一条抛物线把平面分成两部分，两条抛物线最多把平面分成七个部分，设 条抛物线至多把平面分成 个部分，则 （ ）
    A.
    B.
    C.
    D.

    【答案】D
    【解析】一条抛物线将平面至多分为2部分，两条抛物线将平面至多分为7部分，

    设第n条抛物线将平面至多分为f(n)部分,则第n+1条抛物线的情况如下：增加的这条抛物线,与原来的n条抛物线至多有4n个交点(由于抛物线是曲线,所以每两条抛物线至多有4个交点,这4n个交点将第n+1条抛物线分为4n+1个曲线段,这4n+1个曲线段将每个所处的区域一分为二,即比原来增加了4n+1个区域,所以f(n+1)f(n)=4n+1.

    所以答案是：D.


    【考点精析】根据题目的已知条件，利用归纳推理的相关知识可以得到问题的答案，需要掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图四边形ABCD为边长为2的菱形，G为AC与BD交点，平面BED⊥平面ABCD，BE=2，AE=2 ．
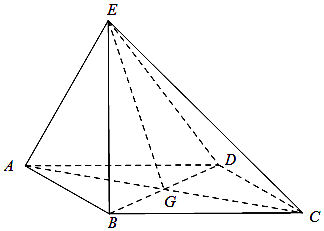
    （Ⅰ）证明：BE⊥平面ABCD；
    （Ⅱ）若∠ABC=120°，求直线EG与平面EDC所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ，若 ， ，使得 ，则实数 的取值范围是( )
    A.(－∞，1]
    B.[1，＋∞)
    C.(－∞，2]
    D.[2，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四名同学根据各自的样本数据研究变量x,y之间的相关关系，并求得回归直线方程和相关系数r，分别得到以下四个结论：
    ① ②
    ③ ④
    其中，一定不正确的结论序号是（ ）
    A.②③
    B.①④
    C.①②③
    D.②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ，且曲线 在点 处的切线斜率为-3.
    （Ⅰ）求 单调区间；
    （Ⅱ）求 的极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市卫生防疫部门为了控制某种病毒的传染，提供了批号分别为 的五批疫苗，供全市所辖的 三个区市民注射，每个区均能从中任选其中一个批号的疫苗接种.
    （1）求三个区注射的疫苗批号中恰好有两个区相同的概率；
    （2）记 三个区选择的疫苗批号的中位数为X，求 X的分布列及期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数 的图象如图所示，则下列函数与其图象相符的是（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l过点P(-1，2)且与两坐标轴的正半轴所围成的三角形面积等于．

    （1）求直线l的方程．

    （2）求圆心在直线l上且经过点M(2,1)，N(4,-1)的圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为(　　)

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案