练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图,已知在正方形ABCD中,有四个全等的直角三角形,设直角三角形的两条直角边的长为a、b,则正方形ABCD的面积为S1=________,4个直角三角形面积的和为S2=________,则S1_______S2(填“≥”“≤”或“=”).据此,我们就可得到一个不等式(用含a、b的式子表示),并且当a______b时,直角三角形变为________时,S1=S2.

    答案：a2+b2   2ab≥a2+b2≥2ab = 等腰直角三角形

    解析：因为直角三角形的直角边长为a、b,

    所以正方形的边长为.而4个直角三角形的面积和为2ab,由图形可知a2+b2≥2ab.

    当直角三角形变为等腰直角三角形,即a=b时,正方形EFGH缩为一个点,这时有a2+b2=2ab.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网（A）（不等式选讲）不等式log3（|x-4|+|x+5|）＞a对于一切x∈R恒成立，则实数a的取值范围是
     
    ；
    （B） （几何证明选讲）如图，已知在△ABC中，∠C=90°，正方形DEFC內接于△ABC，DE∥AC，EF∥BC，AC=1，BC=2，则正方形DEFC的边长等于
     
    ；
    （C） （极坐标系与参数方程）曲线ρ=2sinθ与ρ=2cosθ相交于A，B两点，则直线AB的方程为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：山东省高密市2012届高三5月适应性训练数学理科试题 题型：044

    如图，已知在四棱锥P－ABCD中，底面ABCD是边长为4的正方形，△PAD是正三角形，平面PAD⊥平面ABCD，E、F、G分别是PA、PB、BC的中点．

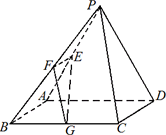
    (Ⅰ)求证：EF⊥平面PAD；

    (Ⅱ)求平面EFG与平面ABCD所成锐二面角的大小；

    (Ⅲ)若M为线段AB上靠近A的一个动点，问当AM长度等于多少时，直线MF与平面EFG所成角的正弦值等于？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    （A）（不等式选讲）不等式log3（|x-4|+|x+5|）＞a对于一切x∈R恒成立，则实数a的取值范围是________；
    （B） （几何证明选讲）如图，已知在△ABC中，∠C=90°，正方形DEFC內接于△ABC，DE∥AC，EF∥BC，AC=1，BC=2，则正方形DEFC的边长等于________；
    （C） （极坐标系与参数方程）曲线ρ=2sinθ与ρ=2cosθ相交于A，B两点，则直线AB的方程为________．

    查看答案和解析>>

    科目：高中数学 来源：2011年陕西省宝鸡市高三质量检测数学试卷2（理科）（解析版） 题型：解答题

    （A）（不等式选讲）不等式log3（|x-4|+|x+5|）＞a对于一切x∈R恒成立，则实数a的取值范围是    ；
    （B） （几何证明选讲）如图，已知在△ABC中，∠C=90°，正方形DEFC內接于△ABC，DE∥AC，EF∥BC，AC=1，BC=2，则正方形DEFC的边长等于    ；
    （C） （极坐标系与参数方程）曲线ρ=2sinθ与ρ=2cosθ相交于A，B两点，则直线AB的方程为    ．

    查看答案和解析>>

    科目：高中数学 来源：2011年陕西省宝鸡市高三质量检测数学试卷2（文科）（解析版） 题型：解答题

    （A）（不等式选讲）不等式log3（|x-4|+|x+5|）＞a对于一切x∈R恒成立，则实数a的取值范围是    ；
    （B） （几何证明选讲）如图，已知在△ABC中，∠C=90°，正方形DEFC內接于△ABC，DE∥AC，EF∥BC，AC=1，BC=2，则正方形DEFC的边长等于    ；
    （C） （极坐标系与参数方程）曲线ρ=2sinθ与ρ=2cosθ相交于A，B两点，则直线AB的方程为    ．

    查看答案和解析>>

    同步练习册答案