
【题目】一个正方形花圃被分成5份.
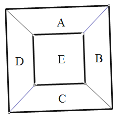
(1)若给这5个部分种植花,要求相邻两部分种植不同颜色的花,己知现有红、黄、蓝、绿4种颜色不同的花,求有多少种不同的种植方法?
(2)若将6个不同的盆栽都摆放入这5个部分,且要求每个部分至少有一个盆栽,问有多少种不同的放法?
【答案】(1)72;(2)1800
【解析】
(1)先对![]() 部分种植,再对
部分种植,再对![]() 部分种植,对
部分种植,对![]() 部分种植进行分类:①若与
部分种植进行分类:①若与![]() 相同,②若与
相同,②若与![]() 不同进行讨论即可;
不同进行讨论即可;
(2)将6个盆栽分成5组,即2-1-1-1-1,将分好的5组全排列即可.
(1)先对![]() 部分种植,有4种不同的种植方法;
部分种植,有4种不同的种植方法;
再对![]() 部分种植,又3种不同的种植方法;
部分种植,又3种不同的种植方法;
对![]() 部分种植进行分类:
部分种植进行分类:
①若与![]() 相同,
相同,![]() 有2种不同的种植方法,
有2种不同的种植方法,![]() 有2种不同的种植方法,共有
有2种不同的种植方法,共有![]() (种),
(种),
②若与![]() 不同,
不同,![]() 有2种不同的种植方法,
有2种不同的种植方法,![]() 有1种不同的种植方法,
有1种不同的种植方法,![]() 有1种不同的种植方法,
有1种不同的种植方法,
共有![]() (种),
(种),
综上所述,共有72种种植方法。
(2)将6个盆栽分成5组,则2-1-1-1-1,有![]() 种分法;
种分法;
将分好的5组全排列,对应5个部分,则一共有![]() (种)放法,
(种)放法,
综上所述,共有1800种不同的放法。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,双曲线![]() (a,b>0)的左右焦点分别为F1(-c,0),F2(c,0),左顶点为A,左准线为l,过F1作直线交双曲线C左支于P,Q两点,则下列命题正确的是( )
(a,b>0)的左右焦点分别为F1(-c,0),F2(c,0),左顶点为A,左准线为l,过F1作直线交双曲线C左支于P,Q两点,则下列命题正确的是( )
A.若PQ⊥x轴,则△PQF2的周长为![]()
B.连PA交l于D,则必有QD//x轴
C.若PQ中点为M,则必有PQ⊥MF2
D.连PO交双曲线C右支于点N,则必有PQ//NF2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有_______.(写出所有正确说法的序号)
①在![]() 中,若
中,若![]() ,则
,则![]() ;
;
②在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形;
是锐角三角形;
③在![]() 中,若
中,若![]() ,则
,则![]() ;
;
④若![]() 是等差数列,其前
是等差数列,其前![]() 项和为
项和为![]() ,则三点
,则三点![]()
![]()
![]() 共线;
共线;
⑤等比数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() ,点
,点![]() 均在函数
均在函数![]() (
(![]() 且
且![]() ,
,![]()
![]() 均为常数)的图象上,则
均为常数)的图象上,则![]() 的值为
的值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角三角形ABC中,![]() ,
,![]() (如右图所示)
(如右图所示)
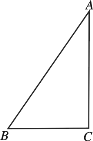
(Ⅰ)若以AC为轴,直角三角形ABC旋转一周,试说明所得几何体的结构特征并求所得几何体的表面积.
(Ⅱ)一只蚂蚁在问题(Ⅰ)形成的几何体上从点B绕着几何体的侧面爬行一周回到点B,求蚂蚁爬行的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,已知A,a,b,给出下列说法:
中,已知A,a,b,给出下列说法:
①若![]() ,则此三角形最多有一解;
,则此三角形最多有一解;
②若![]() ,且
,且![]() ,则此三角形为直角三角形,且
,则此三角形为直角三角形,且![]() ;
;
③当![]() ,且
,且![]() 时,此三角形有两解.
时,此三角形有两解.
其中正确说法的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥M-ABC中,MA=MB=MC=AC=![]() ,AB=BC=2,O为AC的中点,点N在边BC上,且
,AB=BC=2,O为AC的中点,点N在边BC上,且![]() .
.
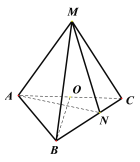
(1)证明:BO![]() 平面AMC;
平面AMC;
(2)求二面角N-AM-C的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com