
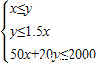 ,所表示的平面区域是以A(
,所表示的平面区域是以A(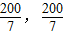 )、B(
)、B(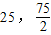 )、O(0,0)为顶点的△AOB的边界及其内部,作直线l:y=-x.由图形可知,把直线l平移至过点B(
)、O(0,0)为顶点的△AOB的边界及其内部,作直线l:y=-x.由图形可知,把直线l平移至过点B(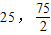 )时,z取最大值.
)时,z取最大值.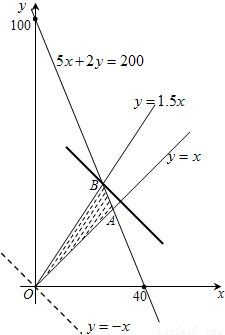 解:设桌子、椅子各买x张和y张,则所买桌椅的总数为z=x+y.
解:设桌子、椅子各买x张和y张,则所买桌椅的总数为z=x+y.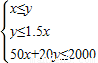 其中x,y∈N+.…(4分)
其中x,y∈N+.…(4分)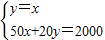 解得
解得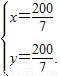
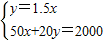 解得
解得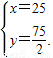 …(6分)
…(6分)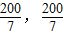 ),点B的坐标为(
),点B的坐标为(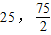 ),
),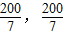 )、
)、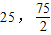 )、O(0,0)为顶点的△AOB的边界及其内部(如图中阴影所示). …(9分)
)、O(0,0)为顶点的△AOB的边界及其内部(如图中阴影所示). …(9分)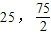 )时,亦即x=25,
)时,亦即x=25,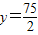 时,z取最大值.
时,z取最大值.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2005年广东省广州市普通高中必修模块调研数学试卷(11月份)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com