
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,
, ![]() (
(![]() 在
在![]() 轴上方),且
轴上方),且![]() .设点
.设点![]() 在
在![]() 轴上的射影为
轴上的射影为![]() ,三角形
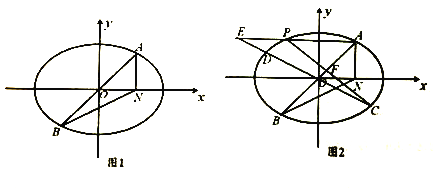
,三角形![]() 的面积为2(如图1).
的面积为2(如图1).
(1)求椭圆的方程;
(2)设平行于![]() 的直线与椭圆相交,其弦的中点为
的直线与椭圆相交,其弦的中点为![]() .
.
①求证:直线![]() 的斜率为定值;
的斜率为定值;
②设直线![]() 与椭圆相交于两点
与椭圆相交于两点![]() ,
, ![]() (
(![]() 在
在![]() 轴上方),点
轴上方),点![]() 为椭圆上异于
为椭圆上异于![]() ,
, ![]() ,
, ![]() ,
, ![]() 一点,直线
一点,直线![]() 交
交![]() 于点
于点![]() ,
, ![]() 交
交![]() 于点
于点![]() ,如图2,求证:
,如图2,求证: ![]() 为定值.
为定值.
【答案】(1)![]() (2) ①
(2) ①![]() ②
②![]()
【解析】试题分析:(1)设![]() ,已知
,已知![]() ,即
,即![]() ,所以
,所以![]() ,故
,故![]() ,即
,即![]() ,再根据椭圆经过
,再根据椭圆经过![]() 解得
解得![]() ,从而可得椭圆的方程;(2)设平行
,从而可得椭圆的方程;(2)设平行![]() 的直线的方程为
的直线的方程为![]() ,且
,且![]() ,① 联立
,① 联立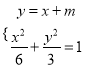 ,得到
,得到![]() ,根据韦达定理求得
,根据韦达定理求得![]() ,
, ![]() ,从而可得直线
,从而可得直线![]() 的斜率为定值,②由题意可知
的斜率为定值,②由题意可知![]() ,求出
,求出![]() .设
.设![]() ,求出
,求出![]() 的坐标,利用弦长公式分别求出
的坐标,利用弦长公式分别求出![]() 的值,将
的值,将![]() 用
用![]() 表示,化简消去
表示,化简消去![]() 即可的结论.
即可的结论.
试题解析:(1)由题意,可设![]() ,已知
,已知![]() ,即
,即![]() ,
,
所以![]() ,故
,故![]() ,即
,即![]() ;
;
又椭圆经过![]() ,即
,即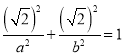 ,解得
,解得![]() ;
;
故所求椭圆的方程为: ![]()
(2)设平行![]() 的直线的方程为
的直线的方程为![]() ,且
,且![]() ,
,
① 联立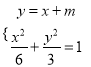 ,得到
,得到![]() ,
,
所以![]() ,
, ![]() ;
;
故,直线![]() 的斜率为
的斜率为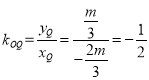 (定值)
(定值)
②由题意可知![]() ,
,
联立方程组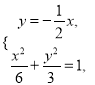 得
得![]()
设![]() ,先考虑直线斜率都存在的情形:
,先考虑直线斜率都存在的情形:
直线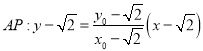 ,
,
联立方程组: 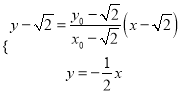 得
得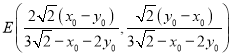 ,
,
直线![]() ,
,
联立方程组: 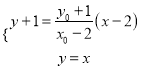 得
得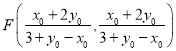 ,
,
则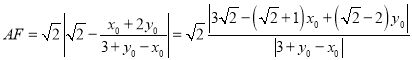 ,
,
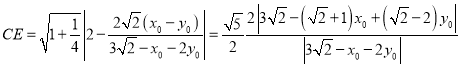 ,
,
所以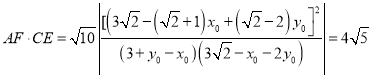
当直线斜率不存在时结果仍然成立.


科目:高中数学 来源: 题型:
【题目】如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.

(1)证明:EM⊥BF;
(2)求平面BEF与平面ABC所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(1)当![]() 时,若函数
时,若函数![]() 与
与![]() 的图象在
的图象在![]() 处有相同的切线,求
处有相同的切线,求![]() 的值;
的值;
(2)当![]() 时,若对任意
时,若对任意![]() 和任意
和任意![]() ,总存在不相等的正实数
,总存在不相等的正实数![]() ,使得
,使得![]() ,求
,求![]() 的最小值;
的最小值;
(3)当![]() 时,设函数
时,设函数![]() 与
与![]() 的图象交于
的图象交于![]()
![]() 两点.求证:
两点.求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥PABCD中,AD∥BC,平面PAC⊥平面ABCD,AB=AD=DC=1,
∠ABC=∠DCB=60,E是PC上一点.
(Ⅰ)证明:平面EAB⊥平面PAC;
(Ⅱ)若△PAC是正三角形,且E是PC中点,求三棱锥AEBC的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随机抽取![]() 人对共享产品对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对共享产品对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的性别以及意见进行了分类,得到的数据如下表所示:
人中的性别以及意见进行了分类,得到的数据如下表所示:
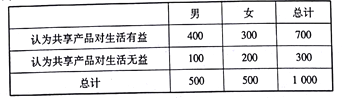
(Ⅰ)根据表中的数据,能否在犯错的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(Ⅱ)为了答谢参与问卷调查的人员,该公司对参与本次问卷调查的人员随机发放![]() 张超市的购物券,购物券金额以及发放的概率如下:
张超市的购物券,购物券金额以及发放的概率如下:
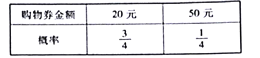
现有甲、乙两人领取了购物券,记两人领取的购物券的总金额为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:  .
.
临界值表:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 经过
经过![]() 为坐标原点,线段
为坐标原点,线段![]() 的中点在圆
的中点在圆![]() 上.
上.
(1)求![]() 的方程;
的方程;
(2)直线![]() 不过曲线
不过曲线![]() 的右焦点
的右焦点![]() ,与
,与![]() 交于
交于![]() 两点,且
两点,且![]() 与圆
与圆![]() 相切,切点在第一象限,
相切,切点在第一象限, ![]() 的周长是否为定值?并说明理由.
的周长是否为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() ,其中
,其中![]() 为参数,且
为参数,且![]() 在直角坐标系
在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 是曲线
是曲线![]() 上的一点,直线
上的一点,直线![]() 被曲线
被曲线![]() 截得的弦长为
截得的弦长为![]() ,求
,求![]() 点的极坐标.
点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从A、B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
A地区: | 62 | 73 | 81 | 92 | 95 | 85 | 74 | 64 | 53 | 76 |
78 | 86 | 95 | 66 | 97 | 78 | 88 | 82 | 76 | 89 | |
B地区: | 73 | 83 | 62 | 51 | 91 | 46 | 53 | 73 | 64 | 82 |
93 | 48 | 95 | 81 | 74 | 56 | 54 | 76 | 65 | 79 |
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度的平均值及分散程度(不要求算出具体值,给出结论即可):

(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,且椭圆的离心率为
上,且椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 为椭圆
为椭圆![]() 的右顶点,点
的右顶点,点![]() 是椭圆
是椭圆![]() 上不同的两点(均异于
上不同的两点(均异于![]() )且满足直线
)且满足直线![]() 与
与![]() 斜率之积为
斜率之积为![]() .试判断直线
.试判断直线![]() 是否过定点,若是,求出定点坐标,若不是,说明理由.
是否过定点,若是,求出定点坐标,若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com