
【题目】已知函数F(x)=g(x)+h(x)=ex , 且g(x),h(x)分别是R上的偶函数和奇函数,若对任意的x∈(0,+∞),不等式g(2x)≥ah(x)恒成立,则实数a的取值范围是( )
A.(﹣∞,2 ![]() ]
]
B.(﹣∞,2 ![]() )
)
C.(﹣∞,2]
D.(﹣∞,2)
【答案】A
【解析】解:∵函数F(x)=ex满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,
∴g(﹣x)=g(x),h(﹣x)=﹣h(x)
∴ex =g(x)+h(x),e﹣x=g(x)﹣h(x),
∴g(x)= ![]() ,h(x)=
,h(x)= ![]() .
.
∵x∈(0,+∞),使得不等式g(2x)≥ah(x)恒成立,即 ![]() ≥a
≥a ![]() 恒成立,
恒成立,
∴a≤ ![]() =(ex﹣e﹣x)+
=(ex﹣e﹣x)+ ![]() ,
,
设t=ex﹣e﹣x , 则函数t=ex﹣e﹣x在(0,+∞)上单调递增,
∴0<t,
此时 不等式t+ ![]() ≥2
≥2 ![]() ,当且仅当t=
,当且仅当t= ![]() ,即t=
,即t= ![]() 时,取等号,∴a≤2
时,取等号,∴a≤2 ![]() ,
,
故选:A.
【考点精析】通过灵活运用函数奇偶性的性质,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇即可以解答此题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1=AB=2,AD=1点E,F,G分别是DD1 , AB,CC1的中点,则异面直线A1E与GF所成的角是( ) 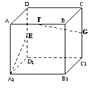
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装,每件服装的成本为40元,出厂单价为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元,根据市场调查,销售商一次订购量不会超过500件.
(1)设一次订购量为x件,服装的实际出厂单价为P元,写出函数P=f(x)的表达式;
(2)当销售商一次订购多少件服装时,该服装厂获得的利润最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线x+ay﹣1=0是圆C:x2+y2﹣4x﹣2y+1=0的对称轴,过点A(﹣4,a)作圆C的一条切线,切点为B,则|AB|=( )
A.2
B.6
C.4 ![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某消费品专卖店的经营资料显示如下:
①这种消费品的进价为每件14元;
②该店月销售量Q(百件)与销售价格P(元)满足的函数关系式为Q= ![]() ,点(14,22),(20,10),(26,1)在函数的图象上;
,点(14,22),(20,10),(26,1)在函数的图象上;
③每月需各种开支4400元.
(1)求月销量Q(百件)与销售价格P(元)的函数关系;
(2)当商品的价格为每件多少元时,月利润最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点. 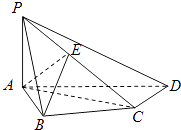
(1)证明CD⊥AE;
(2)证明PD⊥平面ABE;
(3)求二面角A﹣PD﹣C的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ex+1)(ax+2a﹣2),若存在x∈(0,+∞),使得不等式f(x)﹣2<0成立,则实数a的取值范围是( )
A.(0,1)
B.(0, ![]() )
)
C.(﹣∞,1)
D.(﹣∞, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com