
【题目】若函数![]() 在
在![]() 上是单调函数,则a的取值范围是( )
上是单调函数,则a的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【解析】
由求导公式和法则求出f′(x),由条件和导数与函数单调性的关系分类讨论,分别列出不等式进行分离常数,再构造函数后,利用整体思想和二次函数的性质求出函数的最值,可得a的取值范围.
解:由题意得,f′(x)![]() ,
,
因为![]() 在[1,+∞)上是单调函数,
在[1,+∞)上是单调函数,
所以f′(x)≥0或f′(x)≤0在[1,+∞)上恒成立,
①当f′(x)≥0时,则![]() 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,
即a![]() ,设g(x)
,设g(x)![]() ,
,
因为x∈[1,+∞),所以![]() ∈(0,1],
∈(0,1],
当![]() 1时,g(x)取到最大值是:0,
1时,g(x)取到最大值是:0,
所以a≥0,
②当f′(x)≤0时,则![]() 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,
即a![]() ,设g(x)
,设g(x)![]() ,
,
因为x∈[1,+∞),所以![]() ∈(0,1],
∈(0,1],
当![]() 时,g(x)取到最大值是:
时,g(x)取到最大值是:![]() ,
,
所以a![]() ,
,
综上可得,a![]() 或a≥0,
或a≥0,
所以数a的取值范围是(﹣∞,![]() ]∪[0,+∞),
]∪[0,+∞),
故选:B.


科目:高中数学 来源: 题型:
【题目】定义:对棱相等的四面体为等腰四面体.
(1)若等腰四面体的每条棱长都是![]() ,求该等腰四面体的体积;
,求该等腰四面体的体积;
(2)求证:等腰四面体每个面的三角形均为锐角三角形:
(3)设等腰四面体![]() 的三个侧面与底面所成的角分别为
的三个侧面与底面所成的角分别为![]() ,请判断
,请判断![]() 是否为定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
是否为定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有4名学生参加演讲比赛,有![]() 两个题目可供选择,组委会决定让选手通过掷一枚质地均匀的骰子选择演讲的题目,规则如下:选手掷出能被3整除的数则选择
两个题目可供选择,组委会决定让选手通过掷一枚质地均匀的骰子选择演讲的题目,规则如下:选手掷出能被3整除的数则选择![]() 题目,掷出其他的数则选择
题目,掷出其他的数则选择![]() 题目.
题目.
(1)求这4个人中恰好有1个人选择![]() 题目的概率;
题目的概率;
(2)用![]() 分别表示这4个人中选择
分别表示这4个人中选择![]() 题目的人数,记
题目的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知梯形ABCD中,![]() ,如图(1)所示.现将△ABC沿边BC翻折至
,如图(1)所示.现将△ABC沿边BC翻折至![]() A'BC,记二面角A'—BC—D的大小为θ.
A'BC,记二面角A'—BC—D的大小为θ.
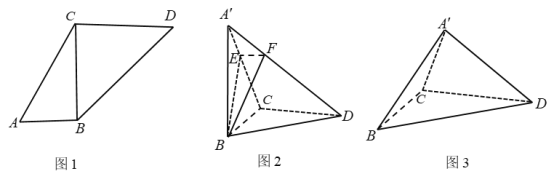
(1)当θ=90°时,如图(2)所示,过点B作平面与A‘D垂直,分别交![]() 于点E,F,求点E到平面
于点E,F,求点E到平面![]() 的距离;
的距离;
(2)当![]() 时,如图(3)所示,求二面角
时,如图(3)所示,求二面角![]() 的正切值
的正切值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国际海洋安全规定:两国军舰正常状况下(联合军演除外),在公海上的安全距离为20![]() (即距离不得小于20
(即距离不得小于20![]() ),否则违反了国际海洋安全规定.如图,在某公海区域有两条相交成60°的直航线
),否则违反了国际海洋安全规定.如图,在某公海区域有两条相交成60°的直航线![]() ,
,![]() ,交点是
,交点是![]() ,现有两国的军舰甲,乙分别在
,现有两国的军舰甲,乙分别在![]() ,
,![]() 上的
上的![]() ,
,![]() 处,起初
处,起初![]() ,
,![]() ,后来军舰甲沿
,后来军舰甲沿![]() 的方向,乙军舰沿
的方向,乙军舰沿![]() 的方向,同时以40
的方向,同时以40![]() 的速度航行.
的速度航行.
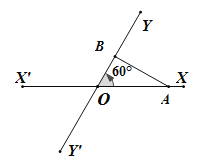
(1)起初两军舰的距离为多少?
(2)试判断这两艘军舰是否会违反国际海洋安全规定?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业共有员工10000人,下图是通过随机抽样得到的该企业部分员工年收入(单位:万元)频率分布直方图.
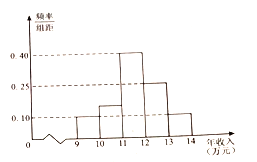
(1)根据频率分布直方图计算样本的平均数.并以此估算该企业全体员工中年收入不低于样本平均数的人数(同一组中的数据以这数据所在区间中点的值作代表);
(2)若抽样调查中收入在![]() 万元员工有2人,求在收入在
万元员工有2人,求在收入在![]() 万元的员工中任取3人,恰有2位员工收入在
万元的员工中任取3人,恰有2位员工收入在![]() 万元的概率;
万元的概率;
(3)若抽样调查的样本容量是400人,在这400人中:年收入在![]() 万元的员工中具有大学及大学以上学历的有
万元的员工中具有大学及大学以上学历的有![]() ,年收入在
,年收入在![]() 万元的员工中不具有大学及大学以上学历的有
万元的员工中不具有大学及大学以上学历的有![]() ,将具有大学及大学以上学历和不具有大学及大学以上学历的员工人数填入下面的列联表,并判断能否有
,将具有大学及大学以上学历和不具有大学及大学以上学历的员工人数填入下面的列联表,并判断能否有![]() 的把握认为具有大学及大学以上学历和不具有大学及大学以上学历的员工收入有差异?
的把握认为具有大学及大学以上学历和不具有大学及大学以上学历的员工收入有差异?
具有大学及大学以上学历 | 不具有大学及大学以上学历 | 合计 | |
| |||
| |||
合计 |
附:![]() ;
;
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com