
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,直线x+y+
,直线x+y+ ![]() =0与椭圆E仅有一个公共点.
=0与椭圆E仅有一个公共点.
(1)求椭圆E的方程;
(2)直线l被圆O:x2+y2=3所截得的弦长为3,且与椭圆E交于A、B两点,求△ABO面积的最大值.
【答案】
(1)解:由 ![]() ,得
,得 ![]() ,即
,即 ![]() ,∴a2=2b2,
,∴a2=2b2,
则椭圆方程为x2+2y2﹣2b2=0.
联立 ![]() ,消去y得,
,消去y得, ![]() ,
,
由 ![]() ,解得:b2=1.
,解得:b2=1.
∴椭圆方程为: ![]()
(2)解:∵直线l被圆O:x2+y2=3所截得的弦长为3,
∴原点O到直线l的距离为 ![]() .
.
①当直线l的斜率不存在时,直线l的方程为x=± ![]() ,代入椭圆
,代入椭圆 ![]() ,得y=
,得y= ![]() ,
,
不妨设A( ![]() ),B(
),B( ![]() ),
),
则 ![]() ;
;
②当直线l的斜率存在时,设直线l的方程为y=kx+m,即kx﹣y+m=0,
由 ![]() ,得4m2=3k2+3.
,得4m2=3k2+3.
联立  ,消去y得,(1+2k2)x2+4kmx+2m2﹣2=0.
,消去y得,(1+2k2)x2+4kmx+2m2﹣2=0.
![]() ,
,
∴|AB|= ![]() =
= ![]() =
= ![]() .
.
设k2=t,
令y= ![]() ,则(4y﹣5)t2+(4y﹣6)t+y﹣1=0,
,则(4y﹣5)t2+(4y﹣6)t+y﹣1=0,
当y= ![]() 时,可得t=
时,可得t= ![]() ,符合题意;
,符合题意;
当y ![]() 时,由△=(4y﹣6)2﹣(4y﹣5)(4y﹣4)≥0,得y
时,由△=(4y﹣6)2﹣(4y﹣5)(4y﹣4)≥0,得y ![]() 且y
且y ![]() .
.
综上,y ![]() .
.
∴当斜率存在时, ![]() =
= ![]() .
.
综①②可知,△ABO面积的最大值为 ![]()
【解析】(1)由椭圆的离心率可得a2=2b2 , 得到椭圆方程x2+2y2﹣2b2=0,联立直线方程和椭圆方程,由判别式等于0求得b2 , 则椭圆方程可求;(2)由直线l被圆O:x2+y2=3所截得的弦长为3,得到坐标原点到直线l的距离为 ![]() ,然后分直线l的斜率存在和不存在两种情况求△ABO面积,当直线l的斜率不存在时,直接求解,当直线l的斜率存在时,设出直线方程y=kx+m,由原点到直线的距离列式,把m用含有k的代数式表示,然后再由弦长公式求得弦长,换元后利用判别式法求得弦长的最大值,求出斜率存在时△ABO面积的最大值,最后比较得答案.
,然后分直线l的斜率存在和不存在两种情况求△ABO面积,当直线l的斜率不存在时,直接求解,当直线l的斜率存在时,设出直线方程y=kx+m,由原点到直线的距离列式,把m用含有k的代数式表示,然后再由弦长公式求得弦长,换元后利用判别式法求得弦长的最大值,求出斜率存在时△ABO面积的最大值,最后比较得答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在五面体ABCDPN中,棱PA⊥面ABCD,AB=AP=2PN,底面ABCD是菱形,∠BAD=![]() .
.

(1)求证:PN∥AB;
(2)求NC与平面BDN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四面体ABCD中,△ABC是正三角形,AD=CD.(12分)
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为 . (参考数据:sin15°=0.2588,sin7.5°=0.1305) 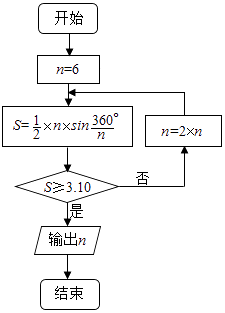
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右两个焦点为
的左右两个焦点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() .
.
(1)求椭圆C的标准方程;
(2)设直线![]() 与椭圆C相交于
与椭圆C相交于![]() 两点,椭圆的左顶点为
两点,椭圆的左顶点为![]() ,连接
,连接![]() 并延长交直线
并延长交直线![]() 于
于![]() 两点 ,
两点 ,![]() 分别为
分别为![]() 的纵坐标,且满足
的纵坐标,且满足![]() .求证:直线
.求证:直线![]() 过定点.
过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com