
【题目】如图,![]() ,
,![]() 是某景区的两条道路(宽度忽略不计,
是某景区的两条道路(宽度忽略不计,![]() 为东西方向),Q为景区内一景点,A为道路
为东西方向),Q为景区内一景点,A为道路![]() 上一游客休息区,已知
上一游客休息区,已知![]() ,
,![]() (百米),Q到直线
(百米),Q到直线![]() ,
,![]() 的距离分别为3(百米),
的距离分别为3(百米),![]() (百米),现新修一条自A经过Q的有轨观光直路并延伸至道路
(百米),现新修一条自A经过Q的有轨观光直路并延伸至道路![]() 于点B,并在B处修建一游客休息区.
于点B,并在B处修建一游客休息区.
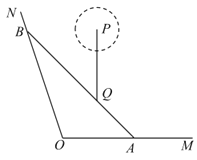
(1)求有轨观光直路![]() 的长;
的长;
(2)已知在景点Q的正北方6百米的P处有一大型组合音乐喷泉,喷泉表演一次的时长为9分钟,表演时,喷泉喷洒区域以P为圆心,r为半径变化,且t分钟时,![]() (百米)(
(百米)(![]() ,
,![]() ).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道
).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道![]() 以
以![]() (百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
(百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
【答案】(1)![]() ;(2)喷泉的水流不会洒到观光车上,理由见解析
;(2)喷泉的水流不会洒到观光车上,理由见解析
【解析】
(1)建立如图平面直角坐标系,易得![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,![]()
![]() ,由点到直线距离,求出
,由点到直线距离,求出![]() ,从而直线
,从而直线![]() 的方程为
的方程为![]() ,联产方程组求出
,联产方程组求出![]() 的坐标,由此能求出轨道的长;
的坐标,由此能求出轨道的长;
(2)将喷泉记为圆![]() ,由题意得
,由题意得![]() ,生成
,生成![]() 分钟时,观光车在线段AB上的点C处,则
分钟时,观光车在线段AB上的点C处,则![]() ,
,![]() ,从而
,从而![]() ,若喷泉不会洒到观光车上,则
,若喷泉不会洒到观光车上,则![]() 对
对![]() 恒成立,由此能求出喷泉的水流不会洒到观光车上.
恒成立,由此能求出喷泉的水流不会洒到观光车上.
(1)以点O为坐标原点,直线![]() 为x轴,建立平面直角坐标系,如图所示.
为x轴,建立平面直角坐标系,如图所示.
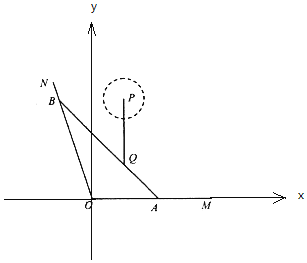
则由题设得:![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,![]() (
(![]() ).
).
由![]() ,解得
,解得![]() ,所以
,所以![]() .
.
故直线![]() 的方程为
的方程为![]() ,
,
由![]() 得
得![]()
即![]() ,故
,故![]() ,
,
答:水上旅游线![]() 的长为
的长为![]() .
.
(2)将喷泉记为圆P,由题意可得![]() ,
,
生成t分钟时,观光车在线段![]() 上的点C处,
上的点C处,
则![]() ,
,![]() ,所以
,所以![]() .
.
若喷泉不会洒到观光车上,则![]() 对
对![]() 恒成立,
恒成立,
即![]() ,
,
当![]() 时,上式成立,
时,上式成立,
当![]() 时,
时,![]() ,
,![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
因为![]() ,所以
,所以![]() 恒成立,即喷泉的水流不会洒到观光车上.
恒成立,即喷泉的水流不会洒到观光车上.
答:喷泉的水流不会洒到观光车上.


科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请120名同学每人随机写下一个x,y都小于1的正实数对
的值:先请120名同学每人随机写下一个x,y都小于1的正实数对![]() ,再统计其中x,y能与1构成钝角三角形三边的数对
,再统计其中x,y能与1构成钝角三角形三边的数对![]() 的个数m,最后根据统计个数m估计
的个数m,最后根据统计个数m估计![]() 的值.如果统计结果是
的值.如果统计结果是![]() ,那么可以估计
,那么可以估计![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:椭圆![]() 的离心率为
的离心率为![]() ,且
,且![]() ,过左焦点
,过左焦点![]() 作一条直线交椭圆于
作一条直线交椭圆于![]() 、
、![]() 两点,过线段
两点,过线段![]() 的中点
的中点![]() 作
作![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() .
.
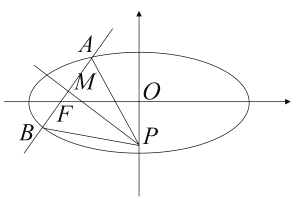
(1)求椭圆方程;
(2)当![]() 面积最大时,求直线
面积最大时,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法上自古以来使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字开始,“地支”以“子”字开始,两者按干支顺序相配,组成了干支纪年法,其相配顺序为:甲子、乙丑、丙寅…癸酉,甲戌、乙亥、丙子…癸未,甲申、乙酉、丙戌…癸巳,…,共得到60个组合,称六十甲子,周而复始,无穷无尽。2019年是“干支纪年法”中的己亥年,那么2026年是“干支纪年法”中的
A. 甲辰年B. 乙巳年C. 丙午年D. 丁未年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市为迎接一项重要的体育赛事,要完成![]() ,
,![]() 两座场馆的地基建造工程.某工程队需要把600名工人分成两组,一组完成
两座场馆的地基建造工程.某工程队需要把600名工人分成两组,一组完成![]() 场馆的甲级标准地基2000
场馆的甲级标准地基2000![]() ,同时另一组完成
,同时另一组完成![]() 场馆的乙级标准地基3000
场馆的乙级标准地基3000![]() ;据测算,完成甲级标准地基每平方米的工程量为50人
;据测算,完成甲级标准地基每平方米的工程量为50人![]() 天,完成乙级标准地基每平方米的工程量为30人
天,完成乙级标准地基每平方米的工程量为30人![]() 天.
天.
(1)若工程队分配![]() 名工人去
名工人去![]() 场馆,求
场馆,求![]() 场馆地基和
场馆地基和![]() 场馆地基建造时间
场馆地基建造时间![]() 和
和![]() (单位:天)的函数解析式;
(单位:天)的函数解析式;
(2)![]() 、
、![]() 两个场馆同时开工,该工程队如何分配两个场馆的工人数量,可以使得工期最短.
两个场馆同时开工,该工程队如何分配两个场馆的工人数量,可以使得工期最短.
(参考数据:![]() ,
,![]() ,
,![]() .备注:若地基面积为
.备注:若地基面积为![]() 平方米,每平方米的工程量为
平方米,每平方米的工程量为![]() 人/天,工人数
人/天,工人数![]() 人,则工期为
人,则工期为![]() 天.)
天.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为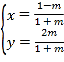 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,过
两点,过![]() 作与
作与![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() 点,若
点,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标xOy中,以O为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(1)求椭圆的直角坐标方程;
(2)已知过![]() 的直线与椭圆C交于A,B两点,且两点与左右顶点不重合,若
的直线与椭圆C交于A,B两点,且两点与左右顶点不重合,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数).在以
为参数).在以![]() 为极点、
为极点、![]() 轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,曲线
轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,曲线![]() :
:![]() 的焦点
的焦点![]() 的极坐标为
的极坐标为![]() .
.
(1)求常数![]() 的值;
的值;
(2)设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com