
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)求证:“如果直线![]() 过点
过点![]() ,那么
,那么![]() ”是真命题;
”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=x ![]() +bx,曲线y=f(x)在点 (2,f(2))处的切线方程为y=(e-1)x+4,
+bx,曲线y=f(x)在点 (2,f(2))处的切线方程为y=(e-1)x+4,
(1)求a,b的值;
(2)求f(x)的单调区间。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A.56
B.60
C.120
D.140
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需确定加工零件所花费的时间,为此做了4次试验,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
若加工时间![]() 与零件个数
与零件个数![]() 之间有较好的相关关系.
之间有较好的相关关系.
(1)求加工时间与零件个数的线性回归方程![]() .
.
(2)试预报加工10个零件需要的时间.
附录:参考公式: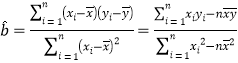 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1 .
(1)求数列{bn}的通项公式;
(2)令cn= ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线x2﹣ ![]() =1的左、右焦点分别为F1、F2 , 若点P在双曲线上,且△F1PF2为锐角三角形,则|PF1|+|PF2|的取值范围是 .
=1的左、右焦点分别为F1、F2 , 若点P在双曲线上,且△F1PF2为锐角三角形,则|PF1|+|PF2|的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(-1,2)且与两坐标轴的正半轴所围成的三角形面积等于![]() .
.
(1)求直线l的方程.
(2)求圆心在直线l上且经过点M(2,1),N(4,-1)的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,正方形![]() 所在的平面与正三角形
所在的平面与正三角形![]() 所在的平面互相垂直,
所在的平面互相垂直, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求面![]() 与面
与面![]() 所成锐二面角的大小.
所成锐二面角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 数列{ ![]() }的公差为1的等差数列,且a2=3,a3=5.
}的公差为1的等差数列,且a2=3,a3=5.
(1)求数列{an}的通项公式;
(2)设bn=an3n , 求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com