
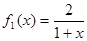 ,定义
,定义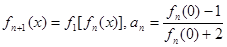 ,其中n∈N*.
,其中n∈N*.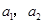 的值,并求证:数列{an}是等比数列;
的值,并求证:数列{an}是等比数列;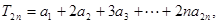
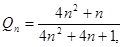 ,其中n∈N*,试比较9
,其中n∈N*,试比较9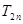 与
与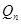 大小,并说明理由.
大小,并说明理由. 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源:不详 题型:解答题
 ,从
,从 上的点
上的点 作
作 轴的垂线,交
轴的垂线,交 于点
于点 ,再从点
,再从点 作
作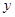 轴的垂线,交
轴的垂线,交 于点
于点 ,设
,设

 的通项公式;
的通项公式;  ,数列
,数列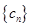 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小
的大小 ;
; ,数列
,数列 的前
的前 项和为
项和为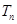 ,试证明:
,试证明: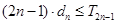

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的
 都有
都有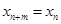 成立,那么就把这样一类数列
成立,那么就把这样一类数列 称作周期为
称作周期为 的周期数列,
的周期数列, 的最小正值称作数列
的最小正值称作数列 的最小正周期,以下简称周期。例如当
的最小正周期,以下简称周期。例如当 时,
时, 是周期为
是周期为 的周期数列;当
的周期数列;当 时,
时, 是周期为
是周期为 的周期数列。设数列
的周期数列。设数列 满足
满足
 .
. 是周期为
是周期为 的周期数列,则常数
的周期数列,则常数 的值是 ;
的值是 ; 的前
的前 项和为
项和为 ,若
,若 ,则
,则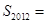 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.42,41,123 | B.13,39,123 |
| C.24,23,123 | D.28,27,123 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com