
分析 (Ⅰ)由正弦定理,三角函数恒等变换的应用化简已知等式可求sin(C-30°)=$\frac{1}{2}$,结合C的范围,利用正弦函数的性质可求C的值.
(Ⅱ)由余弦定理,基本不等式可求ab≤1,进而利用三角形面积公式即可得解.
解答 (本小题满分10分)
解:(Ⅰ)由正弦定理,得$ccosA+\sqrt{3}csinA-b-a=0?sinCcosA+\sqrt{3}sinCsinA=sinB+sinA$,…(1分)
$?sinCcosA+\sqrt{3}sinCsinA=sin(C+A)+sinA$,…(2分)
$?\sqrt{3}sinC-cosC=1?sin(C-30°)=\frac{1}{2}$,…(4分)
?C-30°=30°,(150°舍去),
?C=60°.…(5分)
(Ⅱ)三角形的面积$S=\frac{1}{2}absinC=\frac{{\sqrt{3}}}{4}ab$,…(6分)
由余弦定理,得1=a2+b2-2abcosC=a2+b2-ab,…(8分)
又a2+b2≥2ab,
所以ab≤1,当且仅当a=b时等号成立.
所以,△ABC面积的最大值为$\frac{{\sqrt{3}}}{4}$.…(10分)
点评 本题主要考查了正弦定理,三角函数恒等变换的应用,正弦函数的图象和性质,余弦定理,基本不等式,三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
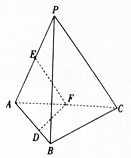 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证:
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,4] | B. | [3,4] | C. | (-∞,0)∪(0,4] | D. | (-∞,-1)∪(0,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -4 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -2 | C. | -4 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{6}$单位即可 | B. | 向右平移$\frac{π}{6}$单位即可 | ||
| C. | 向右平移$\frac{π}{3}$单位即可 | D. | 向左平移$\frac{π}{3}$单位即可 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com