
【题目】如图,多面体![]() 中,
中,![]() 是正方形,
是正方形,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 和平面
和平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析,(2)![]()
【解析】
(1)首先根据已知条件易证![]() 平面
平面![]() ,从而得到
,从而得到![]() ,又根据
,又根据![]() 得到
得到![]() 平面
平面![]() ,根据中位线得到
,根据中位线得到![]() ,得到
,得到![]() 平面
平面![]() ,根据
,根据![]() ,
,![]() 是
是![]() 中点,得到
中点,得到![]() ,再根据线面垂直的判定即可证明
,再根据线面垂直的判定即可证明![]() 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,分别求出平面
轴建立空间直角坐标系,分别求出平面![]() 和平面
和平面![]() 的法向量,再代入二面角公式计算即可.
的法向量,再代入二面角公式计算即可.
(1)因为![]() ,
,![]() ,
,
所以![]() ,即
,即![]() .
.
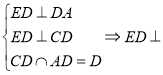 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为四边形![]() 是正方形,所以
是正方形,所以![]() .
.
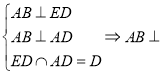 平面
平面![]() .
.
因为![]() ,四边形
,四边形![]() 是正方形,所以
是正方形,所以![]() .
.
又因为![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 的中点,所以
的中点,所以![]() .
.
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() 是
是![]() 中点,所以
中点,所以![]() .
.
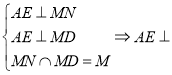 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
如图所示:
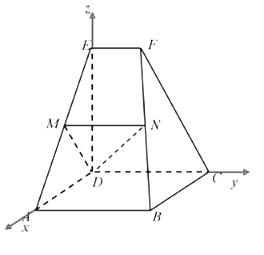
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() ,
,![]()
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由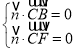 ,得
,得![]() ,令
,令![]() ,则
,则![]() .
.
由(1)可知![]() 平面
平面![]()
所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 和平面
和平面![]() 所成锐二面角为
所成锐二面角为![]() ,
,
则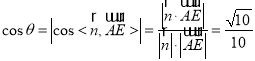
所以平面![]() 和平面
和平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,AD=1,M为AB的中点,将△ADM沿DM翻折.在翻折过程中,当二面角A—BC—D的平面角最大时,其正切值为( )
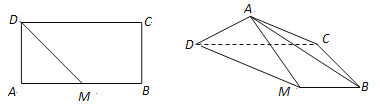
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一布袋中装有![]() 个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
A. 若![]() ,则乙有必赢的策略B. 若
,则乙有必赢的策略B. 若![]() ,则甲有必赢的策略
,则甲有必赢的策略
C. 若![]() ,则甲有必赢的策略D. 若
,则甲有必赢的策略D. 若![]() ,则乙有必赢的策略
,则乙有必赢的策略
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行某种游戏比赛,规定:每一次胜者得1分,负者得0分;当其中一人的得分比另一人的得分多2分时即赢得这场游戏,比赛随之结束.同时规定:比赛次数最多不超过20次,即经20次比赛,得分多者赢得这场游戏,得分相等为和局.已知每次比赛甲获胜的概率为可![]() ,乙获胜的概率为
,乙获胜的概率为![]() .假定各次比赛的结果是相互独立的,比赛经
.假定各次比赛的结果是相互独立的,比赛经![]() 次结束.求
次结束.求![]() 的期望
的期望![]() 的变化范围.
的变化范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列{![]() }的公比为 q(q > 0,q = 1),前 n 项和为 Sn,且 2a1a3 = a4,数列{
}的公比为 q(q > 0,q = 1),前 n 项和为 Sn,且 2a1a3 = a4,数列{![]() }的前 n 项和 Tn 满足2Tn = n(bn - 1),n ∈N*,b2 = 1.
}的前 n 项和 Tn 满足2Tn = n(bn - 1),n ∈N*,b2 = 1.
(1) 求数列 {![]() },{
},{![]() }的通项公式;
}的通项公式;
(2) 是否存在常数 t,使得 {Sn+ ![]() } 为等比数列?说明理由;
} 为等比数列?说明理由;
(3) 设 cn =![]() ,对于任意给定的正整数 k(k ≥2), 是否存在正整数 l,m(k < l < m), 使得 ck,c1,cm 成等差数列?若存在,求出 l,m(用 k 表示),若不存在,说明理由.
,对于任意给定的正整数 k(k ≥2), 是否存在正整数 l,m(k < l < m), 使得 ck,c1,cm 成等差数列?若存在,求出 l,m(用 k 表示),若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
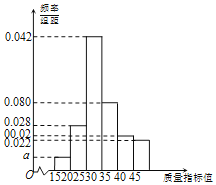
【题目】为保障食品安全,某地食品药监管部门对辖区内甲、乙两家食品企业进行检查,分别从这两家企业生产的某种同类产品中随机抽取了100件作为样本,并以样本的一项关键质量指标值为检测依据.已知该质量指标值对应的产品等级如下:
质量指标值 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45] |
等级 | 次品 | 二等品 | 一等品 | 二等品 | 三等品 | 次品 |
根据质量指标值的分组,统计得到了甲企业的样本频率分布直方图和乙企业的样本频数分布表(如下面表,其中a>0).
质量指标值 | 频数 |
[15,20) | 2 |
[20,25) | 18 |
[25,30) | 48 |
[30,35) | 14 |
[35,40) | 16 |
[40,45] | 2 |
合计 | 100 |
(Ⅰ)现从甲企业生产的产品中任取一件,试估计该件产品为次品的概率;
(Ⅱ)为守法经营、提高利润,乙企业开展次品生产原因调查活动.已知乙企业从样本里的次品中随机抽取了两件进行分析,求这两件次品中恰有一件指标值属于[40,45]的产品的概率;
(Ⅲ)根据图表数据,请自定标准,对甲、乙两企业食品质量的优劣情况进行比较.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() (a>0,b>0)的渐近线方程为y=±
(a>0,b>0)的渐近线方程为y=±![]() x,右顶点为(1,0).
x,右顶点为(1,0).
(1)求双曲线C的方程;
(2)已知直线y=x+m与双曲线C交于不同的两点A,B,且线段AB的中点为![]() ,当x0≠0时,求
,当x0≠0时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别为A1C1和BC的中点.

(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F//平面ABE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com