
【题目】如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.
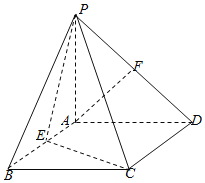
(Ⅰ)求证:AF∥平面PEC;
(Ⅱ)求证:平面PEC⊥平面PCD.
【答案】(Ⅰ)见解析(Ⅱ)见解析
【解析】
(Ⅰ)取PC的中点G,连结FG、EG,AF∥EG又EG平面PCE,AF平面PCE,AF∥平面PCE; (Ⅱ)由(Ⅰ)得EG∥AF,只需证明AF⊥面PDC,即可得到平面PEC⊥平面PCD.
证明:(Ⅰ)取PC的中点G,连结FG、EG,
∴FG为△CDP的中位线,FG∥CD,FG=![]() CD.
CD.
∵四边形ABCD为矩形,E为AB的中点,∴AE∥CD,AE=![]() CD.
CD.
∴FG=AE,FG∥AE,∴四边形AEGF是平行四边形,
∴AF∥EG又EG平面PCE,AF平面PCE,
∴AF∥平面PCE;
(Ⅱ)∵PA=AD.∴AF⊥PD
PA⊥平面ABCD,∴PA⊥CD,
又因为CD⊥AB,AP∩AB=A,∴CD⊥面APD
∴CD⊥AF,且PD∩CD=D,∴AF⊥面PDC
由(Ⅰ)得EG∥AF,∴EG⊥面PDC
又EG平面PCE,∴平面PEC⊥平面PCD.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】七巧板是一种古老的中国传统智力玩具,顾名思义,是由七块板组成的.而这七块板可拼成许多图形.如图中的正方形七巧板就是由五块等腰直角三角形、一块正方形和一块平行四边形组成的.若向正方形内随机的抛10000颗小米粒(大小忽略不计),则落在阴影部分的小米粒大约为( )
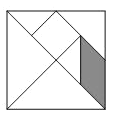
A.3750B.2500C.1875D.1250
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半径为5的圆的圆心在x轴上,圆心的横坐标是整数,且与直线4x+3y﹣29=0相切.
(1)求圆的方程;
(2)设直线ax﹣y+5=0(a>0)与圆相交于A,B两点,求实数a的取值范围;
(3)在(2)的条件下,是否存在实数a,使得弦AB的垂直平分线l过点P(﹣2,4),若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的一个顶点为![]() ,焦点在
,焦点在![]() 轴上,中心在原点.若椭圆短轴的上顶点
轴上,中心在原点.若椭圆短轴的上顶点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆的标准方程;
(2)若椭圆的下顶点为![]() ,设直线
,设直线![]() 与椭圆相交于不同的两点
与椭圆相交于不同的两点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建极坐标系,直线
轴的非负半轴为极轴建极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)射线![]() 与圆C的交点为
与圆C的交点为![]() 与直线
与直线![]() 的交点为
的交点为![]() ,求
,求![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李克强总理在2018年政府工作报告指出,要加快建设创新型国家,把握世界新一轮科技革命和产业变革大势,深入实施创新驱动发展战略,不断增强经济创新力和竞争力.某手机生产企业积极响应政府号召,大力研发新产品,争创世界名牌.为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
单价 |
|
|
|
|
|
|
销量 |
|
|
|
|
|
|
已知![]() .
.
(1)若变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (百件)关于试销单价
(百件)关于试销单价![]() (千元)的线性回归方程
(千元)的线性回归方程![]() ;
;
(2)用(1)中所求的线性回归方程得到与![]() 对应的产品销量的估计值
对应的产品销量的估计值![]() .当销售数据
.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从
称为一个“好数据”.现从![]() 个销售数据中任取
个销售数据中任取![]() 个子,求“好数据”个数
个子,求“好数据”个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(参考公式:线性回归方程中![]() 的估计值分别为
的估计值分别为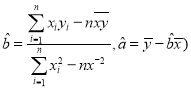 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com