
【题目】已知![]()
(1)求函数![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(2)对一切实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)证明:对一切![]() ,
, ![]() 恒成立.
恒成立.
【答案】(1)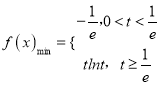 ;(2)4;(3)见解析.
;(2)4;(3)见解析.
【解析】试题分析:(1)求出![]() ,分三种情况讨论,分别令
,分三种情况讨论,分别令 ![]() 得增区间,
得增区间, ![]() 得减区间,从而可得函数
得减区间,从而可得函数![]() 在区间
在区间![]() 上的最小值;(2)
上的最小值;(2)![]() 等价于
等价于![]() ,只需以
,只需以![]() 即可;(3)问题等价于证明
即可;(3)问题等价于证明![]() ,由
,由![]() 的最小值是
的最小值是![]() ,
, ![]() 最大值为
最大值为![]() .
.
试题解析:(1)![]() ,当
,当![]() ,
, ![]() ,
, ![]() 单调递减,当
单调递减,当![]() ,
, ![]() ,
,
![]() 单调递增.············ 2分
单调递增.············ 2分
①![]() ,t无解;
,t无解;
②![]() ,即
,即![]() 时,
时, ![]()
③![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增, ![]()
所以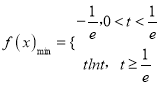 .········· 5分
.········· 5分
(2)![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
, ![]() ,
, ![]() 单调递增,
单调递增, ![]() ,
, ![]() ,
,
![]() 单调递减,所以
单调递减,所以![]() ,因为对一切
,因为对一切![]() ,
, ![]() 恒成立,
恒成立,
所以![]() ;
;
(3)问题等价于证明![]() ,
,
由⑴可知![]() 的最小值是
的最小值是![]() ,当且仅当
,当且仅当![]() 时取到,
时取到,
设![]() ,则
,则![]() ,易得
,易得![]() ,当且仅当
,当且仅当![]() 时取到,从而对一切
时取到,从而对一切![]() ,都有
,都有![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABCDEF.则下列结论不正确的是( )
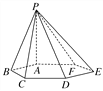
A. CD∥平面PAF
B. DF⊥平面PAF
C. CF∥平面PAB
D. CF⊥平面PAD
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(Ⅰ)当0≤x≤200时,求函数v(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为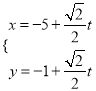 (其中
(其中![]() 为参数),现以坐标原点为极点,
为参数),现以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1中,P,M,N分别为棱DD1,AB,BC的中点.
(1)求二面角B1-MN-B的正切值.
(2)求证:PB⊥平面MNB1.

查看答案和解析>>
科目:高中数学 来源: 题型:
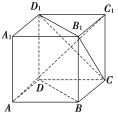
【题目】【2017唐山模拟】如图,ABCDA1B1C1D1为正方体,连接BD,AC1,B1D1,CD1,B1C,现有以下几个结论:①BD∥平面CB1D1;②AC1⊥平面CB1D1;③AC1与底面ABCD所成角的正切值是![]() ;④CB1与BD为异面直线,其中所有正确结论的序号为________.
;④CB1与BD为异面直线,其中所有正确结论的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com