
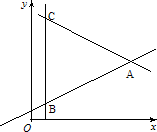
 给出平面区域如图所示,其中A(5,3),B(1,1),C(1,5),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为
给出平面区域如图所示,其中A(5,3),B(1,1),C(1,5),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
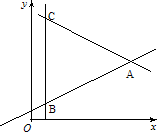 给出平面区域如图所示,其中A(5,3),B(1,1),C(1,5),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )
给出平面区域如图所示,其中A(5,3),B(1,1),C(1,5),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )A、
| ||
B、
| ||
| C、2 | ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
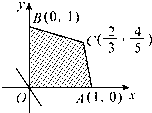 (2007•湛江二模)给出平面区域如图所示,若点C是目标函数z=ax-y取最小值的唯一最优解,则实数a的取值范围是
(2007•湛江二模)给出平面区域如图所示,若点C是目标函数z=ax-y取最小值的唯一最优解,则实数a的取值范围是| 12 |
| 5 |
| 3 |
| 10 |
| 12 |
| 5 |
| 3 |
| 10 |
查看答案和解析>>
科目:高中数学 来源:2012年人教A高数必修五3.3二元一次不等式(组)与简单线性规划问题(解析版) 题型:选择题
给出平面区域如图所示,若使目标函数
 取得最大值的最优解有无穷多个,则
取得最大值的最优解有无穷多个,则 的值为( )
的值为( )
A. B.
B. C.
C. D.
D.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com