
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系(
轴正半轴为极轴,建立极坐标系(![]() ),点
),点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 的延长线上,且满足
的延长线上,且满足![]() ,点
,点![]() 的轨迹为
的轨迹为![]() 。
。
(Ⅰ)求![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)设点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 面积的最小值。
面积的最小值。
【答案】(Ⅰ) ![]() :
:![]() ;
;![]() :
:![]() (Ⅱ)2
(Ⅱ)2
【解析】
(1)由曲线C1的参数方程能求出曲线C1的普通方程,由此能求出曲线C的极坐标方程;设点B的极坐标为(ρ,θ),点A的极坐标为(ρ0,θ0),则|OB|=ρ,|OA|=ρ0,ρ0=2cosθ0,θ=θ0,从而ρρ0=8,由此能求出C2的极坐标方程.
(2)由|OC|=2,S△ABC=S△OBC﹣S△OAC![]() |OC||ρBcosθ﹣ρAcosθ|=|4﹣2cos2θ|,由此能求出S△ABC的最小值.
|OC||ρBcosθ﹣ρAcosθ|=|4﹣2cos2θ|,由此能求出S△ABC的最小值.
(1)∵曲线C1的参数方程为![]() (α为参数),
(α为参数),
∴曲线C1的普通方程为x2+y2﹣2x=0,
∴曲线C的极坐标方程为ρ=2cosθ,
设点B的极坐标为(ρ,θ),点A的极坐标为(ρ0,θ0),
则|OB|=ρ,|OA|=ρ0,ρ0=2cosθ0,θ=θ0,
∵|OA||OB|=8,∴ρρ0=8,
∴![]() ,ρcosθ=4,
,ρcosθ=4,
∴C2的极坐标方程为ρcosθ=4.
(2)由题设知|OC|=2,
S△ABC=S△OBC﹣S△OAC![]() |OC||ρBcosθ﹣ρAcosθ|=|4﹣2cos2θ|,
|OC||ρBcosθ﹣ρAcosθ|=|4﹣2cos2θ|,
当θ=0时,S△ABC取得最小值为2.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系内的动点P到直线![]() 的距离与到点
的距离与到点![]() 的距离比为
的距离比为![]() .
.
(1)求动点P所在曲线E的方程;
(2)设点Q为曲线E与![]() 轴正半轴的交点,过坐标原点O作直线
轴正半轴的交点,过坐标原点O作直线![]() ,与曲线E相交于异于点
,与曲线E相交于异于点![]() 的不同两点
的不同两点![]() ,点C满足
,点C满足![]() ,直线
,直线![]() 和
和![]() 分别与以C为圆心,
分别与以C为圆心,![]() 为半径的圆相交于点A和点B,求△QAC与△QBC的面积之比
为半径的圆相交于点A和点B,求△QAC与△QBC的面积之比![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,下列结论中错误的是
,下列结论中错误的是
A. ![]()
![]() , f(
, f(![]() )=0
)=0
B. 函数y=f(x)的图像是中心对称图形
C. 若![]() 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞,![]() )单调递减
)单调递减
D. 若![]() 是f(x)的极值点,则
是f(x)的极值点,则![]() (
(![]() )=0
)=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄平县且兰高中全体师生努力下,有效进行了“一对一辅导战略”成绩提高了一倍,下列是“优秀学生”,“中等学生”,“差生”进行“一对一”前后所占比例
战略前 | 战略后 | |||||
优秀学生 | 中等学生 | 差生 | 优秀学生 | 中等学生 | 差生 | |
20% | 50% | 30% | 25% | 45% | 30% | |
则下列结论正确的是( )
A.实行“一对一”辅导战略,差生成绩并没有提高.
B.实行“一对一”辅导战略,中等生成绩反而下降了.
C.实行“一对一”辅导战略,优秀学生成绩提高了.
D.实行“一对一”辅导战略,优秀学生与中等生的成绩没有发生改变.
查看答案和解析>>
科目:高中数学 来源: 题型:
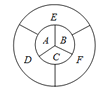
【题目】给图中A,B,C,D,E,F六个区域进行染色,每个区域只染一种颜色,且相邻的区域不同色.若有4种颜色可供选择,则共有___种不同的染色方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com